Question

Source and observer both start moving simultaneously from the origin, one along X axis and the other along Y-axis, the speed of source equal to twice the speed of the observer. The graph between the apparent frequency ($n'$) observed by observer and time $t$ would be: ($n$ is the frequency of the source)
(A)

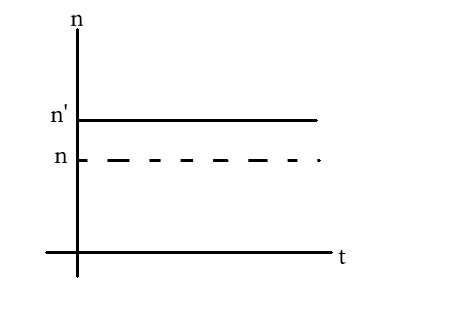
(B)

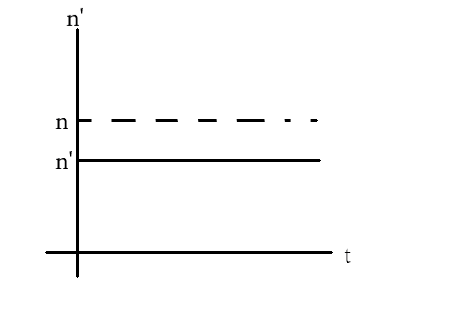
(C)

(D)

Answer 1

We need to find the velocity of the velocity of the observer in the direction of the line joining the source and the observer. Then we need to find the velocity of source in the same direction.

Formula used: In this solution we will be using the following formulae;
$n' = n\left( {\dfrac{{v - {v_L}}}{{v + {v_s}}}} \right)$ where $n'$ is the frequency observed by the observer when the source and observer are moving away from each other, $n$ is the actual frequency of the wave from the source, $v$ is the speed of wave, ${v_L}$ is the speed of the observer and ${v_s}$ is the speed of the source

Complete Step-by-Step Solution:
To find the frequency observed by the observer, we must be able to calculate the actual velocity of recession of the source and observer from each other. Hence, on the line joining the observer and source the component of the velocity of each in that direction is taken as their velocity away from each other.

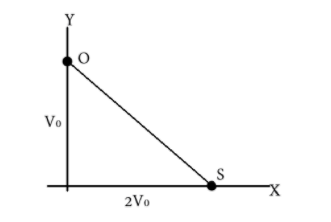
From the diagram, we can see that velocities in the direction of their line of sight can be give each as
${v_L} = {V_0}\cos \theta$ and ${v_s} = 2{V_0}\cos \alpha$
But from Pythagoras theorem
$\cos \theta = \dfrac{1}{{\sqrt 5 }}$ and $\cos \alpha = \dfrac{2}{{\sqrt 5 }}$
Hence,
${v_L} = {V_0}\dfrac{1}{{\sqrt 5 }}$ and ${v_s} = 2{V_0}\dfrac{2}{{\sqrt 5 }}$
The frequency observed when source and observer are moving away from each other is given as
$n' = n\left( {\dfrac{{v - {v_L}}}{{v + {v_s}}}} \right)$ where $n$ is the actual frequency of the wave from the source, $v$ is the speed of wave, ${v_L}$ is the speed of the observer and ${v_s}$ is the speed of the source.
Hence, by inserting into the equation, we have
$n' = n\left( {\dfrac{{v - {V_0}\dfrac{1}{{\sqrt 5 }}}}{{v + 2{V_0}\dfrac{2}{{\sqrt 5 }}}}} \right) = n\left( {\dfrac{{v - \dfrac{{{V_0}}}{{\sqrt 5 }}}}{{v + \dfrac{{4{V_0}}}{{\sqrt 5 }}}}} \right)$
Obviously, $v + \dfrac{{4{V_0}}}{{\sqrt 5 }} > v - \dfrac{{{V_0}}}{{\sqrt 5 }}$
Then, $n' < n$
And as we see, there’s no dependency on time.

Hence, the correct option is B

Note: For clarity, the values of $\cos \theta$ and $\cos \alpha$ can be proven as follows:
Velocity is a vector, hence can be represented as the length of the sides of the triangle as shown in the figure in the solution step. The line of sight is obviously the hypotenuse of the right angled triangle created. Hence,
$v = \sqrt {V_0^2 + {{\left( {2{V_o}} \right)}^2}} = {V_0}\sqrt 5$
Now $\cos \theta = \dfrac{{adjacent}}{{hyp}} = \dfrac{{{V_0}}}{{{V_0}\sqrt 5 }}$
Hence,
$\cos \theta = \dfrac{1}{{\sqrt 5 }}$
Similarly,
$\cos \alpha = \dfrac{2}{{\sqrt 5 }}$