Question

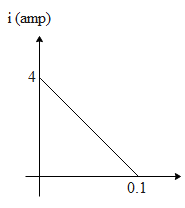
Some magnetic flux is changed in a coil of resistance 10 ohms. As a result an induced current is developed in it which varies with time as shown in the figure. The magnitude of the change in flux through the coil in Weber’s is (Neglect self-inductance of the coil)

a)2
b)4
c)6
d)8

Answer 1

In the above question we are given the variation of current with time in the graph across a coil of resistance 10 ohms. First we will define the change in flux in terms of induced emf across the coil. Further we will express it in terms of resistance of the coil and accordingly obtain the change in flux for the above given conditions.

Formula used:
$\dfrac{d\varphi }{dt}=-E$
$E=iR$

Complete step by step answer:
Let us say we have a coil in which the current changes with time. Let us say for that small change in time the flux across the cross sectional area of the coil changes by $d\varphi$. If at a particular instance of time with respect to the initial the induced emf is ‘E’, we can write the rate of change of flux with time as induced emf. Mathematically this can be represented as,
$\dfrac{d\varphi }{dt}=-E$
If the emf E across a particular coil of resistance ‘R’ is applied. Then by ohms law we can say that current ‘I’ in the circuit is proportional to the ratio of the two. Mathematically this can be represented as,
$E=iR$
Substituting this in the above equation of induced emf we get,
$\begin{aligned} & \dfrac{d\varphi }{dt}=-iR \\\ & \Rightarrow d\varphi =-iRdt \\\ \end{aligned}$
Integrating the above equation we get,
$\int{d\varphi }=R\int{-idt}$ .The integration of the factor (–idt) represents the area under the curve of variation of current with time. This from the above graph we get as 0.2 which is area of triangle, hence from the above equation we get change in flux i.e. $\varphi$ as,
$\begin{aligned} & \varphi =R(0.2) \\\ & \Rightarrow \varphi =10(0.2)=2Wb \\\ \end{aligned}$

So, the correct answer is “Option a”.

Note: In the above solution we have not considered the minus sign in integration as the area under the curve itself is negative as the slope of the curve being negative. The basic idea in solving the question was one has to write the equation of change in flux in terms of resistance of the coil. Then further we can accordingly determine the flux change by setting the limits of current for a given time.