Question
Question: Some energy levels of a molecule are shown in fig. The ratio of the wavelengths \(r = {\lambda _1}/{...
Some energy levels of a molecule are shown in fig. The ratio of the wavelengths r=λ1/λ2is given by:
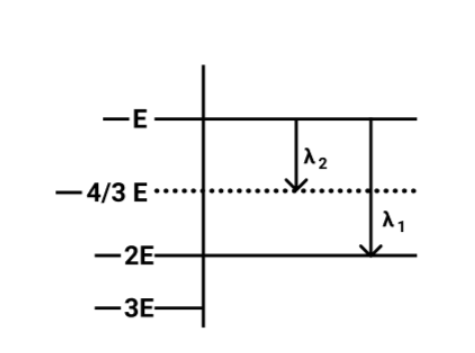
(a) r=31
(b) r=34
(c) r=32
(d) r=43
Solution
we have been given two wavelengths and here are the two transitions. So assuming the corresponding two these two transitions, there is the emission of photons in each case. So firstly we will find the energy of that particular photon then using the relation which we have given in the formula, we will find the ratio between these two wavelengths.
Formula used
The energy of photons,
E=λhc
Here,
E, will be the energy
h, will be the planck's constant
c, will be the speed of light
λ, will be the wavelength
Complete Step By Step Solution: As we know the formula for the energy of the photon and it can be written as
E=λhc
And from here, λcan be written as
⇒λ=Ehc
And hence we can say that
⇒λ∝E1
Now from the figure,
The energy of a photon of wavelength λ2will be equal to
⇒△E2=−E−(−34)
On solving the above equation, we get
⇒△E2=3E
Now we will calculate the Energy of the photon of wavelength λ1 and it will equal to
⇒△E1=−E−(−2E)
On solving the above equation, we get
⇒△E1=E
So now we will calculate the ratios between the two energies
Therefore, it can be written as
⇒λ2λ1=△E1△E2
Now on substituting the values, we get
⇒λ2λ1=E(3E)
So we will solve the final above equation to get the required ratios
⇒r=λ2λ1=31
Therefore, the option awill be the correct choice.
Note: According to Einstein's equation E=mc2 anything that possesses energy has mass and anything that has mass has energy which is equal to the mass of the particle times square of the speed of light. Photons have 0 rest mass but they have Energy which is equal to Planck constant times its frequency. So, if the photon has a fixed amount of energy which will be more than zero with zero rest mass but the photon does not exist which has 0 moving mass so its energy will be zero.
