Question

Solving systems of quadratic inequalities. How to solve a system of quadratic inequalities, using a double number line?

Answer 1

In this question, we have been asked to solve the system of quadratic inequalities using double number-line. We can solve a system of quadratic inequalities in one variable by using a double number-line. In order to solve this question, first we take an example for a system of quadratic inequalities and then find the roots of the equation and then show it on the number line. Later by combining both the number-lines, we will find out the combined solution set and we will get our required solution.

Complete step by step solution:
We can solve a system of quadratic inequalities in one variable by using a double number-line.
For example:
Let assume we have given the two quadratic equation,
$\Rightarrow f(x)={{x}^{2}}+2x-3<0$----- (1)
$\Rightarrow g(x)={{x}^{2}}-4x-5<0$----- (2)
Now, solving the first quadratic equation,
$\Rightarrow f(x)={{x}^{2}}+2x-3<0$
Solving the equation by splitting the middle term, we get
$\Rightarrow {{x}^{2}}+3x-1x-3<0$
Taking out common factors by making pairs, we obtain
$\Rightarrow x\left( x+3 \right)-1\left( x+3 \right)<0$
$\Rightarrow \left( x-1 \right)\left( x+3 \right)<0$
Solving each factor individually equals to 0, we get
$\Rightarrow x-1=0$ And $x+3=0$
$\Rightarrow x=1$ And $x=-3$
Therefore, we the two real roots are 1 and -3.
Thus between -3 and 1, the quadratic function f(x) < 0.
Number line of this function;

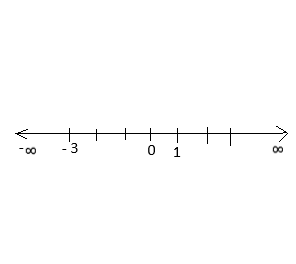
Now, solving the second quadratic equation,
$\Rightarrow g(x)={{x}^{2}}-4x-5<0$
Solving the equation by splitting the middle term, we get
$\Rightarrow {{x}^{2}}-5x+1x-5<0$
Taking out common factors by making pairs, we obtain
$\Rightarrow x\left( x-5 \right)+1\left( x-5 \right)<0$
$\Rightarrow \left( x-5 \right)\left( x+1 \right)<0$
Solving each factor individually equals to 0, we get
$\Rightarrow x-5=0$ And $x+1=0$
$\Rightarrow x=5$ And $x=-1$
Therefore, we the two real roots are 5 and -1
Thus between -1 and 5, the quadratic function g(x) < 0.
Number line of this function,

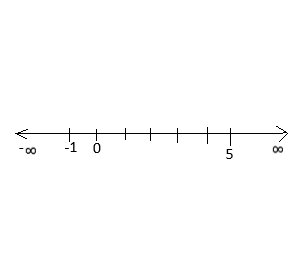
Now, combining the two number lines, we get a combined solution.
The combined solution set of the given system of quadratic equations is open interval (-1, 1).
Thus, in this way we can solve the quadratic inequalities using the double number line.

Note: Students should remember that the real solutions to the system of quadratic inequality become boundary points for the solution to the quadratic inequality. To solve the quadratic inequalities using double number-line, first we need to draw a number line to find out the interval of the particular equation. Similarly done with the second equation. Later by superimposing we get the combined solution set for the system of quadratic equations.