Question

Solve $x^2y''-3xy'+5y=0.$

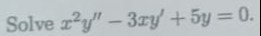
Answer 1

The general solution is: $y = x^2 (C_1 \cos(\ln x) + C_2 \sin(\ln x))$

Answer 2

The given differential equation is a Cauchy-Euler equation. The standard approach involves assuming a solution of the form $y = x^m$. Substituting this into the equation results in a characteristic quadratic equation for $m$. Solving this quadratic equation yields the roots $m = 2 \pm i$. Since the roots are complex conjugates of the form $\alpha \pm i\beta$, the general solution is $y = x^\alpha (C_1 \cos(\beta \ln x) + C_2 \sin(\beta \ln x))$, which for $\alpha=2$ and $\beta=1$ becomes $y = x^2 (C_1 \cos(\ln x) + C_2 \sin(\ln x))$.