Question
Question: Solve: $(x^{2} + y^{2})dx + xy(d(x+y)) = 0$...
Solve: (x2+y2)dx+xy(d(x+y))=0
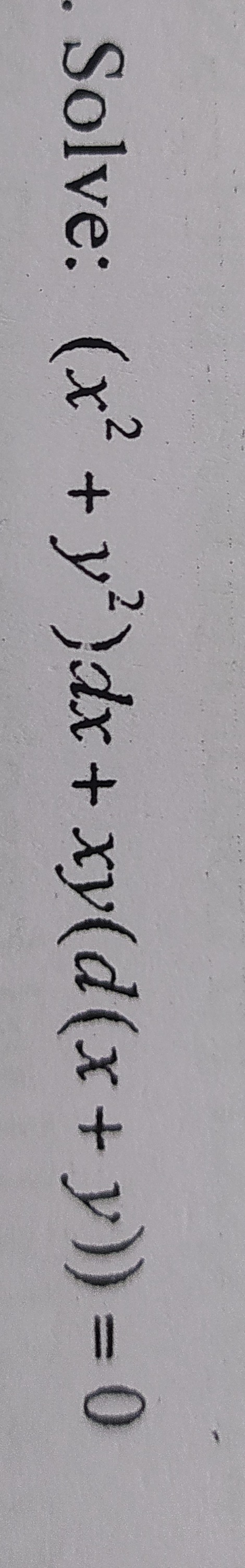
ln(x2(x2+xy+2y2))+72arctan(y72x+y)=C
Solution
The given differential equation is (x2+y2)dx+xy(d(x+y))=0.
First, expand d(x+y) as dx+dy: (x2+y2)dx+xy(dx+dy)=0 (x2+y2)dx+xydx+xydy=0 (x2+xy+y2)dx+xydy=0
This is a homogeneous differential equation because both M(x,y)=x2+xy+y2 and N(x,y)=xy are homogeneous functions of degree 2.
To solve a homogeneous differential equation, we can use the substitution x=vy. Then, dx=vdy+ydv.
Substitute x=vy and dx=vdy+ydv into the equation: ((vy)2+(vy)y+y2)(vdy+ydv)+(vy)ydy=0 (v2y2+vy2+y2)(vdy+ydv)+vy2dy=0 Factor out y2: y2(v2+v+1)(vdy+ydv)+vy2dy=0 Divide by y2 (assuming y=0): (v2+v+1)(vdy+ydv)+vdy=0 Distribute the terms: v(v2+v+1)dy+y(v2+v+1)dv+vdy=0 (v3+v2+v)dy+y(v2+v+1)dv+vdy=0 Combine terms with dy: (v3+v2+v+v)dy+y(v2+v+1)dv=0 (v3+v2+2v)dy+y(v2+v+1)dv=0 v(v2+v+2)dy+y(v2+v+1)dv=0
Separate the variables: ydy=−v(v2+v+2)v2+v+1dv
Integrate both sides: ∫ydy=−∫v(v2+v+2)v2+v+1dv
For the integral on the right-hand side, use partial fraction decomposition: Let v(v2+v+2)v2+v+1=vA+v2+v+2Bv+C Multiply by v(v2+v+2): v2+v+1=A(v2+v+2)+(Bv+C)v v2+v+1=Av2+Av+2A+Bv2+Cv v2+v+1=(A+B)v2+(A+C)v+2A
Comparing coefficients:
- 2A=1⟹A=1/2
- A+C=1⟹1/2+C=1⟹C=1/2
- A+B=1⟹1/2+B=1⟹B=1/2
So, the integrand becomes: v1/2+v2+v+21/2v+1/2=2v1+2(v2+v+2)v+1
Now, integrate: ln∣y∣=−∫(2v1+2(v2+v+2)v+1)dv ln∣y∣=−21∫v1dv−21∫v2+v+2v+1dv
For the second integral, notice that the derivative of the denominator v2+v+2 is 2v+1. We can rewrite the numerator v+1 as 21(2v+2)=21(2v+1+1). So, ∫v2+v+2v+1dv=∫v2+v+221(2v+1)+21dv=21∫v2+v+22v+1dv+21∫v2+v+21dv
The first part of this integral is 21ln∣v2+v+2∣. For the second part, complete the square in the denominator: v2+v+2=v2+v+(21)2−(21)2+2=(v+21)2+47 So, 21∫(v+21)2+(27)21dv=21⋅271arctan(27v+21)=71arctan(72v+1)
Putting it all together: ln∣y∣=−21ln∣v∣−21[21ln∣v2+v+2∣+71arctan(72v+1)]+C1 ln∣y∣=−21ln∣v∣−41ln∣v2+v+2∣−271arctan(72v+1)+C1
Multiply by 4: 4ln∣y∣=−2ln∣v∣−ln∣v2+v+2∣−72arctan(72v+1)+4C1 ln(y4)=ln(v−2)+ln((v2+v+2)−1)−72arctan(72v+1)+C2 ln(y4)=ln(v2(v2+v+2)1)−72arctan(72v+1)+C2 ln(y4v2(v2+v+2))=C2−72arctan(72v+1)
Now substitute back v=x/y: v2=x2/y2 v2+v+2=x2/y2+x/y+2=(x2+xy+2y2)/y2 y4(y2x2)(y2x2+xy+2y2)=x2(x2+xy+2y2)
So the solution becomes: ln(x2(x2+xy+2y2))=C−72arctan(72(x/y)+1) ln(x2(x2+xy+2y2))=C−72arctan(y72x+y)
The final answer is ln(x2(x2+xy+2y2))+72arctan(y72x+y)=C.
