Solveeit Logo
Login

Question

Question: Solve: $(x^2 + 3x + 1)(x^2 + 3x - 3) \geq 5$...

Solve: (x2+3x+1)(x2+3x−3)≥5(x^2 + 3x + 1)(x^2 + 3x - 3) \geq 5

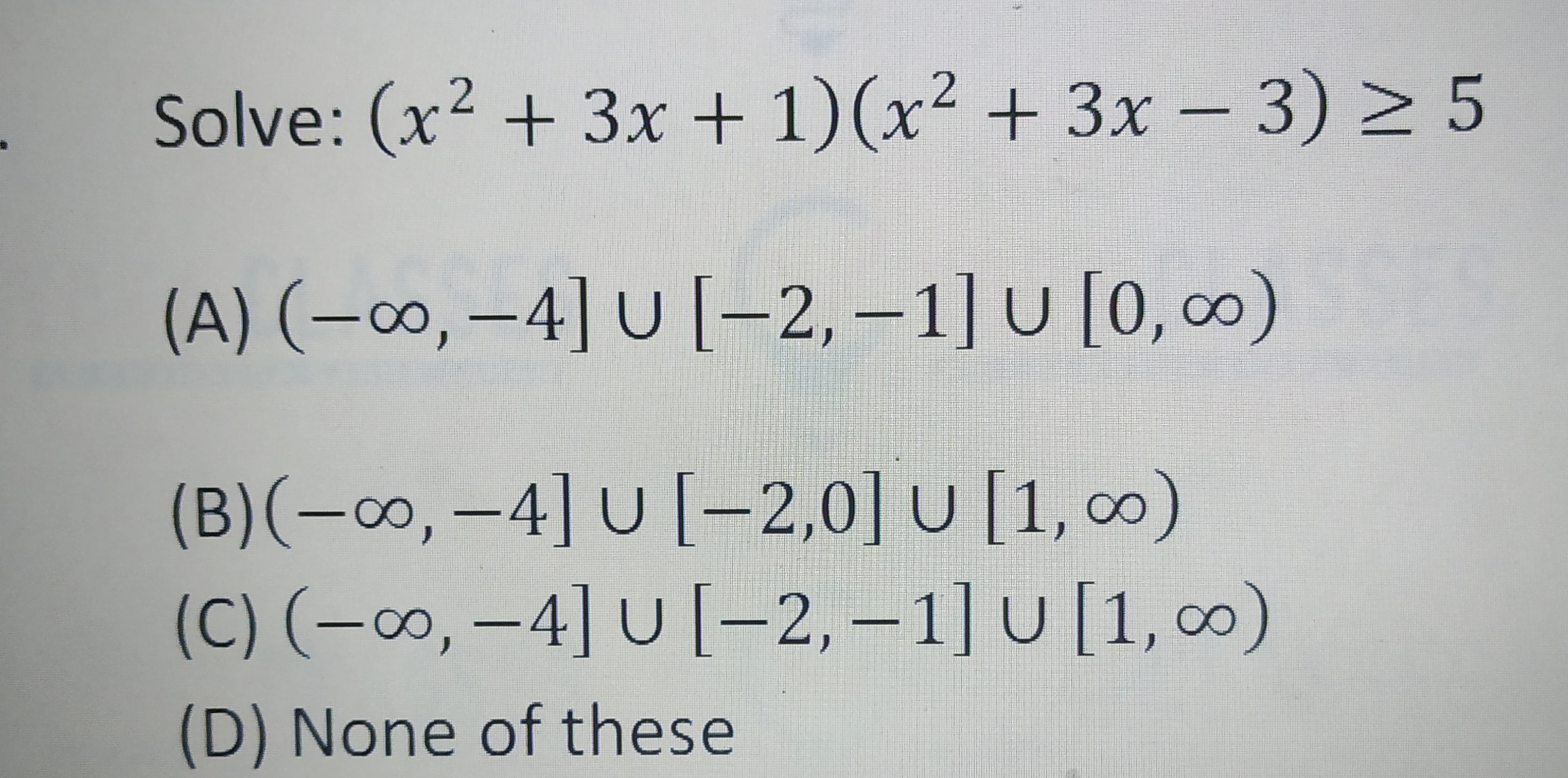
A

(−∞,−4]∪[−2,−1]∪[0,∞)(-\infty, -4] \cup [-2, -1] \cup [0, \infty)

B

(−∞,−4]∪[−2,0]∪[1,∞)(-\infty, -4] \cup [-2,0] \cup [1, \infty)

C

(−∞,−4]∪[−2,−1]∪[1,∞)(-\infty, -4] \cup [-2, -1] \cup [1, \infty)

D

None of these

Answer

(−∞,−4]∪[−2,−1]∪[1,∞)(-\infty, -4] \cup [-2, -1] \cup [1, \infty)

Explanation

Solution

Let y=x2+3xy = x^2 + 3x. The inequality becomes (y+1)(y−3)≥5(y+1)(y-3) \geq 5, which simplifies to y2−2y−8≥0y^2 - 2y - 8 \geq 0. Factoring gives (y−4)(y+2)≥0(y-4)(y+2) \geq 0. This holds when y≤−2y \leq -2 or y≥4y \geq 4.

Case 1: x2+3x≤−2  ⟹  x2+3x+2≤0  ⟹  (x+1)(x+2)≤0x^2 + 3x \leq -2 \implies x^2 + 3x + 2 \leq 0 \implies (x+1)(x+2) \leq 0. The roots are -2 and -1. The solution is −2≤x≤−1-2 \leq x \leq -1.

Case 2: x2+3x≥4  ⟹  x2+3x−4≥0  ⟹  (x+4)(x−1)≥0x^2 + 3x \geq 4 \implies x^2 + 3x - 4 \geq 0 \implies (x+4)(x-1) \geq 0. The roots are -4 and 1. The solution is x≤−4x \leq -4 or x≥1x \geq 1.

The total solution is the union of the solutions from Case 1 and Case 2: (−∞,−4]∪[−2,−1]∪[1,∞)(-\infty, -4] \cup [-2, -1] \cup [1, \infty).