Question

Solve this following inequality:
$\sin x > -\dfrac{1}{2}$
(a) $2n\pi -\dfrac{\pi }{3} < x < 2n\pi +\dfrac{7\pi }{3};n\in \mathbb{Z}$
(b) $2n\pi -\dfrac{\pi }{5} < x < 2n\pi +\dfrac{6\pi }{5};n\in \mathbb{Z}$
(c) $2n\pi -\dfrac{\pi }{4} < x < 2n\pi +\dfrac{5\pi }{4};n\in \mathbb{Z}$
(d) $2n\pi -\dfrac{\pi }{6} < x < 2n\pi +\dfrac{7\pi }{6};n\in \mathbb{Z}$

Answer 1

We solve this problem first by finding the exact solution then we can find the general solution.
We use the condition that the period for sine function is $2\pi$ so that we find the solution in the domain $\left[ -2\pi, 2\pi \right]$ of one complete curve that satisfies the given inequality then we can find the general solution.
For finding the exact solution we use graph theory that is if $f\left( x \right) > g\left( x \right)$ then the solution is given by plotting the graph of $y=f\left( x \right)$ and $y=g\left( x \right)$ such that the domain above the intersection of both graphs will be the solution.
The general solution for a sine function of one complete curve such that the curve of $y=\sin x$ is above the line $y=-\dfrac{1}{2}$ is given by adding the $2n\pi$where $'n'$ is an integer to exact solution because the period of the sine function is $2\pi$

Complete step-by-step solution
We are given with the inequality that is
$\sin x > -\dfrac{1}{2}$
We know that the period of sine function is $2\pi$ so that the exact solution will be in the domain $\left[ -2\pi ,2\pi \right]$
Let us use the graph theory to find the exact solution.
We know that if $f\left( x \right) > g\left( x \right)$ then the solution is given by plotting the graph of $y=f\left( x \right)$ and $y=g\left( x \right)$ such that the domain above the intersection of both graphs will be the solution.
Now, let us plot the graphs $y=\sin x$ and $y=-\dfrac{1}{2}$ then we get

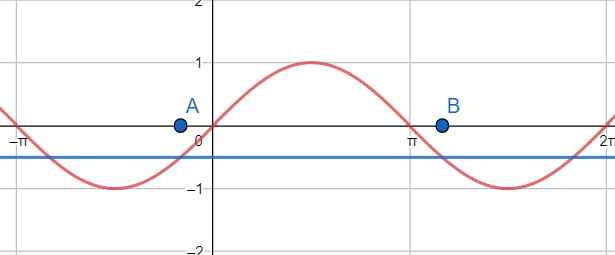
Here we can see that one complete curve of $y=\sin x$ that is above the line $y=-\dfrac{1}{2}$ is located between that points A and B where the co – ordinates of points are $A\left( \dfrac{-\pi }{6},\dfrac{-1}{2} \right),B\left( \dfrac{7\pi }{6},\dfrac{-1}{2} \right)$
So, we can say that the exact solution lies between these points.
So, by converting the above statement into mathematical inequality we get
$\Rightarrow \dfrac{-\pi }{6} < x < \dfrac{7\pi }{6}$
We know that the general solution of sine function is given by adding the $2n\pi$where $'n'$ is an integer to exact solution because the period of the sine function is $2\pi$
So, by adding the $2n\pi$ in above equation we get
$\Rightarrow 2n\pi -\dfrac{\pi }{6} < x < 2n\pi +\dfrac{7\pi }{6};n\in \mathbb{Z}$
So, option (d) is the correct answer.

Note: We can find the exact solution without using the graph theory.
We are given the inequality that is
$\sin x > -\dfrac{1}{2}$
We know that the sine function is negative in the third and fourth quadrants.
So, we can take one value in this and one value in the fourth quadrant such that $\sin x=-\dfrac{1}{2}$ and then we can change it into inequality by taking the value of $'x'$ between those two values.
We know that if $\sin x=-\dfrac{1}{2}$ then $x=\dfrac{-\pi }{6}$ is solution in fourth quadrant and $x=\dfrac{7\pi }{6}$ in third quadrant.
So, we can take the inequality as
$\Rightarrow \dfrac{-\pi }{6} < x < \dfrac{7\pi }{6}$
So, by adding the $2n\pi$ in the above equation we get
$\Rightarrow 2n\pi -\dfrac{\pi }{6} < x < 2n\pi +\dfrac{7\pi }{6};n\in \mathbb{Z}$
So, option (d) is the correct answer.