Solveeit Logo
Login

Question

Question: Solve the modulus equation: \[\left| \dfrac{{{x}^{2}}-8x+12}{{{x}^{2}}-10x+21} \right|=\dfrac{-\l...

Solve the modulus equation:
∣x2−8x+12x2−10x+21∣=−(x2−8x+12)x2−10x+21\left| \dfrac{{{x}^{2}}-8x+12}{{{x}^{2}}-10x+21} \right|=\dfrac{-\left( {{x}^{2}}-8x+12 \right)}{{{x}^{2}}-10x+21}

Explanation

Solution

Hint: First of all, find the values at which the modulus function will change its sign by substituting x2−8x+12=0 and x2−10x+21=0{{x}^{2}}-8x+12=0\text{ and }{{x}^{2}}-10x+21=0. Now divide the number line into various intervals and check for each interval and solve the equation to get the solution. Also, remember that ∣x∣=x for x>0\left| x \right|=x\text{ for }x>0 and ∣x∣=−x for x<0\left| x \right|=-x\text{ for }x<0.

Complete step-by-step answer:
In this question, we have to solve the modulus equation
∣x2−8x+12x2−10x+21∣=−(x2−8x+12)x2−10x+21\left| \dfrac{{{x}^{2}}-8x+12}{{{x}^{2}}-10x+21} \right|=\dfrac{-\left( {{x}^{2}}-8x+12 \right)}{{{x}^{2}}-10x+21}
Let us find the values at which the modulus function will change its signs.
x2−8x+12=0{{x}^{2}}-8x+12=0
We can also write the above equation as,
x2−6x−2x+12=0{{x}^{2}}-6x-2x+12=0
⇒x(x−6)−2(x−6)=0\Rightarrow x\left( x-6 \right)-2\left( x-6 \right)=0
(x−6)(x−2)=0\left( x-6 \right)\left( x-2 \right)=0
So, from this we get x = 6 or x = 2
x2−10x+21=0{{x}^{2}}-10x+21=0
We can also write the above equation as,
x2−7x−3x+21=0{{x}^{2}}-7x-3x+21=0
⇒x(x−7)−3(x−7)=0\Rightarrow x\left( x-7 \right)-3\left( x-7 \right)=0
(x−3)(x−7)=0\left( x-3 \right)\left( x-7 \right)=0
So, from this we get, x = 3 and x = 7.
Now, let us consider the function given in the question
∣x2−8x+12x2−10x+21∣=−(x2−8x+12)x2−10x+21\left| \dfrac{{{x}^{2}}-8x+12}{{{x}^{2}}-10x+21} \right|=\dfrac{-\left( {{x}^{2}}-8x+12 \right)}{{{x}^{2}}-10x+21}
We can also write the above equation as,
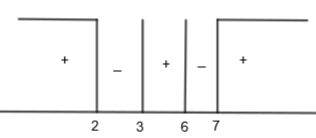
∣(x−6)(x−2)(x−7)(x−3)∣=−(x−6)(x−2)(x−7)(x−3)....(i)\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}....\left( i \right)

Now, we will check the values of the function at different intervals. Also x≠3,7x\ne 3,7 because that will make the denominator 0 which is not possible. We also know that ∣x∣=x\left| x \right|=x where x > 0 and ∣x∣=−x\left| x \right|=-x where x < 0. Let us take x > 7.
For x > 7, (x – 6) > 0, (x – 2) > 0, (x – 7) > 0, (x – 3) > 0
(x−6)(x−2)(x−7)(x−3)>0\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}>0
∣(x−6)(x−2)(x−7)(x−3)∣=(x−6)(x−2)(x−7)(x−3)\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
By using this in equation (i), we get,
(x−6)(x−2)(x−7)(x−3)=−(x−6)(x−2)(x−7)(x−3)\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
Also, x≠7 and x≠3x\ne 7\text{ and }x\ne 3. So, by canceling the denominators, we get,
(x−6)(x−2)=−(x−6)(x−2)\left( x-6 \right)\left( x-2 \right)=-\left( x-6 \right)\left( x-2 \right)
(x−6)(x−2)+(x−6)(x−2)=0\left( x-6 \right)\left( x-2 \right)+\left( x-6 \right)\left( x-2 \right)=0
2(x−6)(x−2)=02\left( x-6 \right)\left( x-2 \right)=0
(x−6)(x−2)=0\left( x-6 \right)\left( x-2 \right)=0
From this, we get, x = 6 or x = 2. But we have to take an interval x > 7. So, x could not be equal to 2 or 6. Similarly, let us take 6≤x<76\le x<7.
For, 6≤x<7,(x−6)>0,(x−2)>0,(x−7)<0,(x−3)>06\le x<7,\left( x-6 \right)>0,\left( x-2 \right)>0,\left( x-7 \right)<0,\left( x-3 \right)>0
So, (x−6)(x−2)(x−7)(x−3)<0\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}<0
∣(x−6)(x−2)(x−7)(x−3)∣=−(x−6)(x−2)(x−7)(x−3)\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
By using this in equation (i), we get,
−(x−6)(x−2)(x−7)(x−3)=−(x−6)(x−2)(x−7)(x−3)\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
As x≠7 and x≠3x\ne 7\text{ and }x\ne 3. So, by canceling the denominator, we get,
−(x−6)(x−2)+(x+6)(x−2)=0-\left( x-6 \right)\left( x-2 \right)+\left( x+6 \right)\left( x-2 \right)=0
0 = 0
LHS = RHS
Since we have got LHS = RHS, that means all the values of this interval will satisfy the equation. So, we get, x∈[6,7)....(i)x\in [6,7)....\left( i \right)
Let us take 3 < x < 6.
For, 3 < x < 6, (x – 6) < 0, (x – 2) > 0, (x – 7) < 0, (x – 3) > 0
(x−6)(x−2)(x−7)(x−3)>0\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}>0
∣(x−6)(x−2)(x−7)(x−3)∣=(x−6)(x−2)(x−7)(x−3)\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
By using this in equation (i), we get,
(x−6)(x−2)(x−7)(x−3)=−(x−6)(x−2)(x−7)(x−3)\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
As x≠7 and x≠3x\ne 7\text{ and }x\ne 3. So, by canceling the denominator, we get,
(x−6)(x−2)=−(x−6)(x−2)\left( x-6 \right)\left( x-2 \right)=-\left( x-6 \right)\left( x-2 \right)
(x−6)(x−2)+(x−6)(x−2)=0\left( x-6 \right)\left( x-2 \right)+\left( x-6 \right)\left( x-2 \right)=0
2(x−6)(x−2)=02\left( x-6 \right)\left( x-2 \right)=0
(x−6)(x−2)=0\left( x-6 \right)\left( x-2 \right)=0
From this, we get, x = 6 or x = 2. But we have to take interval 3 < x < 6, so x could not be equal to 2 or 6.
Let us take 2≤x<32\le x<3
For, 2≤x<3,(x−6)<0,(x−2)>0,(x−7)<0,(x−3)<02\le x<3,\left( x-6 \right)<0,\left( x-2 \right)>0,\left( x-7 \right)<0,\left( x-3 \right)<0
So,
(x−6)(x−2)(x−7)(x−3)<0\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}<0
So,
∣(x−6)(x−2)(x−7)(x−3)∣=−(x−6)(x−2)(x−7)(x−3)\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
By using this in equation (i), we get,
−(x−6)(x−2)(x−7)(x−3)=−(x−6)(x−2)(x−7)(x−3)\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
As x≠7 and x≠3x\ne 7\text{ and }x\ne 3. So, by canceling the denominator, we get,
−(x−6)(x−2)+(x+6)(x−2)=0-\left( x-6 \right)\left( x-2 \right)+\left( x+6 \right)\left( x-2 \right)=0
0=00=0
LHS = RHS
Since we have got LHS = RHS, that means all the values of this interval will satisfy the equation.
So, we get, x∈[2,3)....(ii)x\in [2,3)....\left( ii \right)
Now, let us take x < 2
For, x < 2, (x – 6) < 0, (x – 2) < 0, (x – 7) < 0, (x – 3) < 0
So,
(x−6)(x−2)(x−7)(x−3)>0\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}>0
So,
∣(x−6)(x−2)(x−7)(x−3)∣=(x−6)(x−2)(x−7)(x−3)\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
By using this in equation (i), we get,
(x−6)(x−2)(x−7)(x−3)=(x−6)(x−2)(x−7)(x−3)\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}
As x≠7 and x≠3x\ne 7\text{ and }x\ne 3. So, by canceling the denominator, we get,
(x−6)(x−2)=−(x−6)(x−2)\left( x-6 \right)\left( x-2 \right)=-\left( x-6 \right)\left( x-2 \right)
(x−6)(x−2)+(x−6)(x−2)=0\left( x-6 \right)\left( x-2 \right)+\left( x-6 \right)\left( x-2 \right)=0
2(x−6)(x−2)=02\left( x-6 \right)\left( x-2 \right)=0
(x−6)(x−2)=0\left( x-6 \right)\left( x-2 \right)=0
From this we get x = 6 or x = 2. But we have to take the interval x < 2, so x could not be equal to 2 or 6.
So, from (i) and (ii), we get,
x∈[2,3)∪[6,7)x\in [2,3)\cup [6,7)

Note: Here, students can cross-check their answer by substituting any value of x from [2,3)∪[6,7)[2,3)\cup [6,7) and checking if LHS = RHS. Also, students must note that whenever we get LHS = RHS after solving the equation, then that equation is true for all the values of x in the domain of the equation that we have taken. Also, we can only cancel factors from LHS and RHS of the equation, if they are not equal to zero otherwise we may miss some roots.