Question
Question: solve the integration of root (tanx)...
solve the integration of root (tanx)
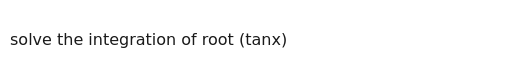
21arctan(2tanxtanx−1)+221lntanx+2tanx+1tanx−2tanx+1+C
Solution
To solve the integral ∫tanxdx, we use a specific substitution and algebraic manipulation.
1. Substitution: Let I=∫tanxdx. Let t2=tanx. Differentiating both sides with respect to x: 2tdxdt=sec2x. We know that sec2x=1+tan2x. Substituting t2=tanx, we get sec2x=1+(t2)2=1+t4. So, 2tdxdt=1+t4, which implies dx=1+t42tdt.
Substitute t2=tanx and dx=1+t42tdt into the integral: I=∫t⋅1+t42tdt=∫1+t42t2dt.
2. Decompose the Integrand: We can split the integrand t4+12t2 into two parts: t4+12t2=t4+1t2+1+t2−1=t4+1t2+1+t4+1t2−1. So, the integral becomes: I=∫t4+1t2+1dt+∫t4+1t2−1dt.
3. Evaluate the First Integral: Let I1=∫t4+1t2+1dt. Divide the numerator and denominator by t2: I1=∫t2+1/t21+1/t2dt. Let u=t−1/t. Then du=(1+1/t2)dt. Also, u2=(t−1/t)2=t2+1/t2−2, so t2+1/t2=u2+2. Substitute these into I1: I1=∫u2+2du=∫u2+(2)2du. This is a standard integral of the form ∫x2+a2dx=a1arctan(ax). I1=21arctan(2u)+C1. Substitute back u=t−1/t=tt2−1: I1=21arctan(2tt2−1)+C1.
4. Evaluate the Second Integral: Let I2=∫t4+1t2−1dt. Divide the numerator and denominator by t2: I2=∫t2+1/t21−1/t2dt. Let v=t+1/t. Then dv=(1−1/t2)dt. Also, v2=(t+1/t)2=t2+1/t2+2, so t2+1/t2=v2−2. Substitute these into I2: I2=∫v2−2dv=∫v2−(2)2dv. This is a standard integral of the form ∫x2−a2dx=2a1lnx+ax−a. I2=221lnv+2v−2+C2. Substitute back v=t+1/t=tt2+1: I2=221lntt2+1+2tt2+1−2+C2=221lnt2+2t+1t2−2t+1+C2.
5. Combine and Substitute Back: Combine I1 and I2: I=I1+I2=21arctan(2tt2−1)+221lnt2+2t+1t2−2t+1+C. Finally, substitute back t2=tanx and t=tanx: I=21arctan(2tanxtanx−1)+221lntanx+2tanx+1tanx−2tanx+1+C.
The final answer is 21arctan(2tanxtanx−1)+221lntanx+2tanx+1tanx−2tanx+1+C.
Explanation of the solution:
- Substitute t2=tanx to transform the integral into a rational function of t: ∫1+t42t2dt.
- Decompose the integrand 1+t42t2 into t4+1t2+1+t4+1t2−1.
- For ∫t4+1t2+1dt, divide numerator and denominator by t2 and substitute u=t−1/t. This leads to an arctan function.
- For ∫t4+1t2−1dt, divide numerator and denominator by t2 and substitute v=t+1/t. This leads to a ln function.
- Combine the results and substitute back t=tanx.
Answer: The integral of tanx is 21arctan(2tanxtanx−1)+221lntanx+2tanx+1tanx−2tanx+1+C.
