Question

Solve the inequality $\dfrac{{3x}}{5} - \dfrac{{\left( {2x - 1} \right)}}{3} > 1$ , $x \in R$ and represent the solution set on the number line.

Answer 1

Inequality is a relation which makes a non-equal comparison between two numbers or mathematical expressions. By using it we can compare two numbers on the number line by their size. It builds a relationship like greater than $( > )$ , greater than equal to $( \geqslant )$ or less than $( < )$ or less than equal to $( \leqslant )$ between two numbers or algebraic expression. In simple words it is used to compare two values. It shows a particular mathematical expression in which the sides are not equal to each other.
Inequalities can be solved by applying similar rules like linear equations.
Using the number line we can plot the different values of $x$ .

Complete step-by-step solution:
Given inequality,
$\dfrac{{3x}}{5} - \dfrac{{\left( {2x - 1} \right)}}{3} > 1$
L.C.M. of $5$ and $3$is $= 5 \times 3$ ; Since $5$ and $3$ are prime to each other.
In other words H.C.F. of $5$ and $3$ is $1$ .
After taking L.C.M. we get,
$\dfrac{{3x \times 3 - \left( {2x - 1} \right) \times 5}}{{15}} > 1$
$\Rightarrow\dfrac{{9x - 10x + 5}}{{15}} > 1$
$\Rightarrow\dfrac{{5 - x}}{{15}} > 1$
After multiplying both sides of the inequality by $15$ , we get
$\Rightarrow 5 - x > 15$
Now after subtracting $15$ from both sides of the inequality, we get
$\Rightarrow 5 - x - 15 > 15 - 15$
$\Rightarrow 5 - x - 15 > 0$
Adding $x$ both sides, we get
$\Rightarrow 5 - x - 15 + x > x$
$\Rightarrow 5 - 15 > x$
$\Rightarrow - 10 > x$
$\Rightarrow x < \- 10$
Therefore the solution set on the number line,

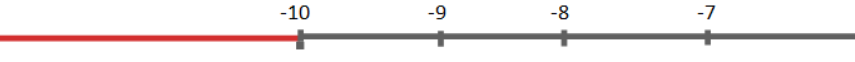
The red spotted line denotes the solution set on the number line.

Note: We should know that multiplying or dividing an inequality by a negative number changes the inequality symbol. It is better to avoid it as it brings more complications . To avoid complication we try to solve the given problem without multiplying or dividing the inequality by a negative number .
Number line is usually represented horizontally.
When the numbers are not relatively prime to each other i.e. the H.C.F. of two numbers is not equals to 1 we have to find out the L.C.M. by Prime factorization method or division method.
We know,
If there are two numbers $a$ and $b$ , and their H.C.F. is known to us then,
$L.C.M. = \dfrac{{a \times b}}{{H.C.F.}}$ ; We can find L.C.M. by using this formula if H.C.F. is known to us. In this sum it is given that H.C.F. is one , so it became easier to take out the L.C.M.