Question

Solve the inequality $- 3 \leqslant 3 - 2x < 9,x \in R.$ represent the solution on a number line.

Answer 1

To solve this type of inequality first divide this inequality into two parts: left inequality and right inequality. After splitting into two try to solve in terms of $x$ only. And then try to represent those points on a number line and apply the conditions to all and try to find the intersection of both the inequalities.

Complete step-by-step solution:
Given,
$- 3 \leqslant 3 - 2x < 9,x \in R.$
So let's divide the inequality into two parts
$- 3 \leqslant 3 - 2x < 9 = 3 - 2x \geqslant - 3\,and\,3 - 2x < 9$
Inequality (i) is
$3 - 2x \geqslant - 3$ ………...……(i)
Inequality (ii) is
$\,3 - 2x < 9$ ………………………(ii)
Solving inequation (i)
$3 - 2x \geqslant - 3$
On further arranging
$- 2x \geqslant - 3 - 3$
$\Rightarrow - 2x \geqslant - 6$
On multiplying by $-$ the inequality will change from greater then to less then
$2x \leqslant 6$
$\Rightarrow x \leqslant 3$ …………………………………(iii)
Now solving inequality (ii)
$\,3 - 2x < 9$
$\Rightarrow \, - 2x < 9 - 3$
$\Rightarrow \, - 2x < 6$
On multiplying by $-$ the inequality will change from greater then to less then
$\,2x > - 6$
$\Rightarrow \,x > \dfrac{{ - 6}}{2}$
$\Rightarrow \,x > - 3$ ……………………(iv)
Equation (iii) says that $x$ is less than or equal to $3$ and equation (iv) says that $x$ is greater than $- 3$.
On applying the condition of equation (iii) and (iv) on the number line look like the given fig.

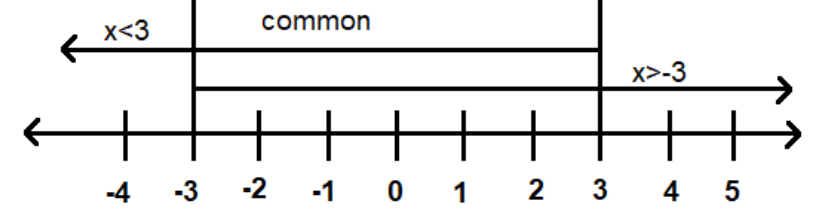
Solution of the given equation is $- 3 < x \leqslant 3$. If $x$ is out of this range then the inequality does not hold good. If we put the value of $x$ out of range in the main inequality then some unexpected answers are coming that are not accepted by mathematics.

Note: To solve this type of question you must know the knowledge of inequality and how we represent that inequality in one number line. Take a look while multiplying with the $-$ sign because if you multiply by the $-$ sign then inequality will change from greater then to less than. At last, we have to take the intersection of both the inequalities.