Question

Solve the given equation graphically:
${{\text{x}}^2} + {\text{x - 2 = 0}}$.

Answer 1

Hint: To find the solution of the given equation, we split the equation into two terms. We plot their graphs individually and compute their points of intersection. The x-coordinates of the points of intersection are the solutions.

Complete step-by-step solution -
Given Data,
${{\text{x}}^2} + {\text{x - 2 = 0}}$
$\Rightarrow {{\text{x}}^2} - \left( {{\text{2 - x}}} \right) = 0 \\\ \Rightarrow {{\text{x}}^2} = 2 - {\text{x}} \\\$
Let y = ${{\text{x}}^2} = 2 - {\text{x}}$
Hence y = ${{\text{x}}^2}$and y =$2 - {\text{x}}$. Let us plot the graphs of these equations, we get

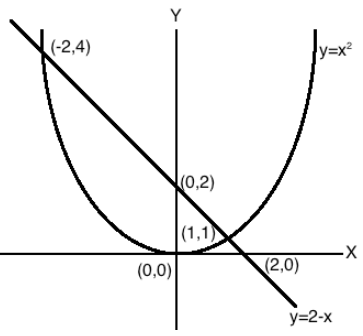
From the graph we can observe that y = ${{\text{x}}^2}$and y =$2 - {\text{x}}$ intersect at points (-2, 4) and (1, 1).
Hence, the solution of the equation ${{\text{x}}^2} + {\text{x - 2 = 0}}$ is x = -2 and 1.

Note: In order to solve this type of questions the key is to plot an appropriate graph for the given equation. We plot the graphs of these equations by substituting random values in x and computing y. We join all these obtained points (x, y) to form a curve or a line depending upon its equation. It is important to realize the solution of the given equation is only the x-coordinates of the points of intersection.