Question

Solve the given algebraic expression ${{\left( x-1 \right)}^{n}}={{x}^{n}}$, where n is a positive integer.

Answer 1

Hint: First assume 2 functions randomly. Now assign the left-hand side and right-hand side to each function. Now find possibilities of n to cover the whole range of n. Now find the value of function at x = 0. Plot the point. Now tell about the way the plot goes in the positive x-axis, negative x-axis. And then plot the way you described. Now repeat this process to other cases also. So, now you have graphs for all cases where n covers the whole possible values of n. Now find the number of solutions in each case. In question, they asked to solve. So, report the number of solutions corresponding to the range of n considered to get the required result.

Complete step-by-step solution -
Given condition in the question, can be written in form of, ${{\left( x-1 \right)}^{n}}={{x}^{n}}$ $n\in$ positive integer.
Assume 2 functions namely f (x), g (x) to solve this question.
Now assume that f (x) is a function in the left-hand side.
Next, assume that g (x) is a function on the right-hand side.
So, by writing values of f (x), simply we get the equation:
$f\left( x \right)={{\left( x-1 \right)}^{n}}$
By writing value of g (x), simply we get the equation as:
$g\left( x \right)={{x}^{n}}$
Given that n is a positive integer. So, to cover the whole range we take 2 cases, n is odd and n is even.
Case 1: First consider that n is even. So, f (x), g (x) vary at x = 0, f (x) = 1, g (x) = 0 as n is even functions are always positive. The reflection to a line parallel to y. So, we can draw them as,

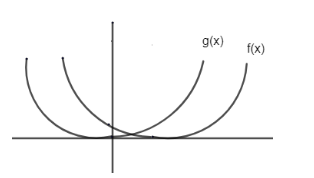
At x = 0, f (x) = 1, g (x) = 0; at x = 1 f (x) = 0 g (x) = 1.
So, there must be a root in between f(x) and g(x).
Case 2: If n is odd then the graph is reflection at one point at x = 0, f (x) = -1, g (x) = 0 and at x=1, f(x)=0 and g(x)=1.
So, no root

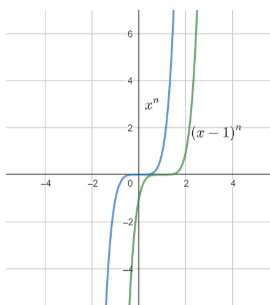
So, 1 root when n is even and no root when n is odd.

Note: Take all cases such that every possible n must be included. The idea of reflection analysis to draw a plot is very important. Students confuse and think about how to draw. By shifting points, we can draw these graphs easily. By transformation, if you pull to origin to (1, 0) what graph you set that must be f (x). Use this transformation idea when the constant difference is there.