Question

Solve the following system of inequalities graphically $x + y \leqslant 9,y > x,x \geqslant 0$.

Answer 1

Hit – In this question plot the different inequalities given onto a single graph paper. First plot the straight line x + y=9, then a straight line passing through origin x=y and then search for the portion on graph for which $x \geqslant 0$ satisfies. Find the points of intersection and mark the regions that satisfy individual inequality, find the region in common.

Complete step-by-step solution -

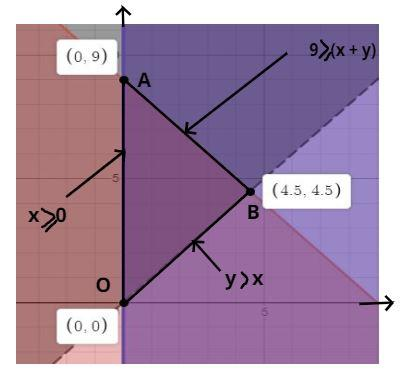
Given system of inequalities
$x + y \leqslant 9,y > x,x \geqslant 0$
Now we have to solve these inequalities graphically.
So plot these inequalities as above.
So the solution of these inequalities is a triangle OAB as shown in figure.
Whose coordinates are also shown in the above figure.
The solution of $x + y \leqslant 9,y > x$ is point B whose coordinates is (4.5, 4.5).
We can also solve this manually when inequalities hold the equation becomes
x + y = 9 and y = x
$\Rightarrow 2x = 9$
$\Rightarrow x = \dfrac{9}{2} = 4.5 = y$
So the coordinates of point B is (4.5, 4.5)
The solution of $x + y \leqslant 9,x \geqslant 0$ is point A whose coordinates is (0, 9).
We can also solve this manually when inequalities hold the equation becomes
x + y = 9 and x = 0
$\Rightarrow 0 + y = 9$
$\Rightarrow y = 9$
So the coordinates of point A is (0, 9).
The solution of $y > x,x \geqslant 0$ is point O whose coordinates is (0, 0).
We can also solve this manually when inequalities hold the equation becomes
y = x and x = 0
$\Rightarrow y = x = 0$
So the coordinates of point O is (0, 0).
So this is the required solution of the system of inequalities.

Note – The graphical plotting of inequalities is mandatory while solving problems of this kind. Here the question arise that why have we plotted x + y=9 and y=x although we needed to solve $x + y \leqslant 9,y > x$, this is because the inequality depicts area however the line depicts the boundary of this area, thus to track this area its boundary needs to be sketched.