Question

Solve the following problem graphically:
Minimise and Maximise –
$z = 3x + 9y \\\ \text{subject to the constraints}: \\\ x + 3y \leqslant 60 \\\ x + y \geqslant 10 \\\ x \leqslant y \\\ x \geqslant 0,y \geqslant 0 \\\$

Answer 1

In this case the function given is to be represented on the graph. The conditions represented by the lines greater than less than can be shaded using any color. The intersection points of the lines on graphical representation can be utilized to find maximum and minimum.

Complete step-by-step solution:
The equation given to Maximise or Minimise
$z = 3x + 9y$
$subject\,to\,the\,constra\operatorname{int} s: \\\ x + 3y \leqslant 60 \\\ x + y \geqslant 10 \\\ x \leqslant y \\\ x \geqslant 0,y \geqslant 0$
For,
$x + 3y \leqslant 60$
At x=0, y=20
X=60, y=0
For,
$x + y \geqslant 10$
At, x=0, y=10
X=10, y=0
For,
$x \leqslant y$
At, x=0, y=0
X=20, y=20
The corner points as we can see in the graph below,
At (0,10) value of z is 90
At (5,5) value of z is 60
At (15.15) value of z is 180
At (0,20) value of z is 180

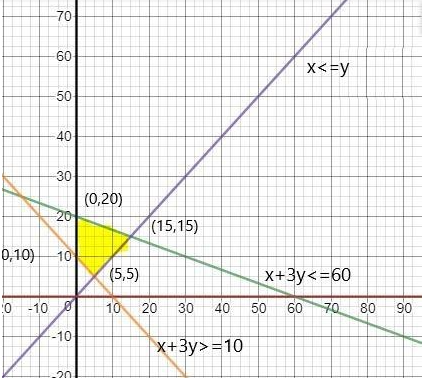
So, we can conclude that,
z=60, is minimum at (5,5)
z=180, is maximum at (15,15) and (0,20).

Note: In this we can find the maximum and minimum by using linear programming. It is better practice to shade the required area in order to understand the corner points of the z. We need to put the corner points and get the values of z in order to maximise and minimise the function.