Question

Solve the following Linear Programming Problems graphically:
Minimize: Z = x + 2y subjected to $2x + y \geqslant 3$, $x + 2y \geqslant 6$, and $x,y \geqslant 0$.

Answer 1

Hint: Draw the lines for the equations,$2x + y \geqslant 3$, $x + 2y \geqslant 6$, and $x,y \geqslant 0$. And shade the region for the given inequality and then find the common region. Find the corner points of the common region and evaluate the value of Z at each of these points and find the minimum value.

Complete step-by-step answer:

We need to maximize Z = x + 2y subjected to the given constraints as follows graphically:
$2x + y \geqslant 3$
$x + 2y \geqslant 6$
$x \geqslant 0$
$y \geqslant 0$
For the first equation, we have as follows:
$2x + y = 3$
We plot the line with the following points:

x	y
0	3
1	1

Since the origin (0,0) does not satisfy the inequality, we shade away from the origin.For the second equation, we have as follows:
$x + 2y = 6$
We plot the line with the following points:

x	y
0	3
6	0

Since the origin (0,0) does not satisfy the inequality, we shade away from the origin.
For $x \geqslant 0$ and $y \geqslant 0$ it just represents the first quadrant, hence, we have the graph as follows:

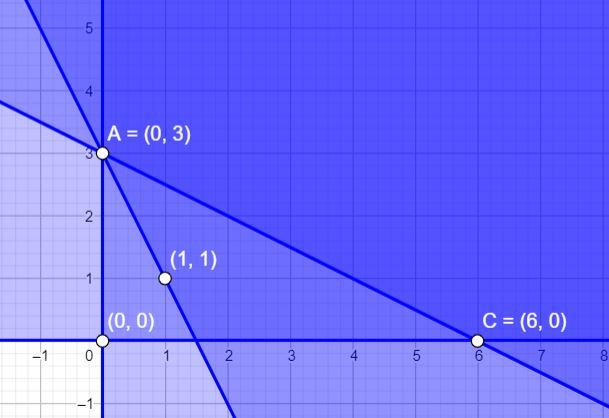
The corner points are A and C. We evaluate Z at these points:

Points	Z = x +2 y
A (0, 3)	6
C (6, 0)	6

Both the points have the same value for Z, hence, the entire line joining the two points A (0, 3) and C (6, 0) are the solutions for the required conditions.

Note: You can cross-check the answer for the given point by substituting in the constraint equations and check if they satisfy the inequality, if they don’t then, there is some mistake in the graphing.Linear programming is used for obtaining the most optimal solution for a problem with given constraints. In linear programming, we formulate our real-life problem into a mathematical model. It involves an objective function, linear inequalities with subject to constraints.