Question

Solve the following linear programming problems graphically:
1. Maximize $Z=3x+4y$ Subject to constraints: $x+y\le 4,x\ge 0,y\ge 0$
2. Minimize $Z=-3x+4y$ Subject to constraints: $x+2y\le 8,3x+2y\le 12,x\ge 0,y\ge 0$

Answer 1

There are 2 parts to this question. Both have to be done in the same way. We will first draw a graph of the given subjects for the constraints and then we will shade the region common to all the inequalities. It will be our required graph. Then we will note down the corner points of that shaded region and put them into Z, one by one. For part-1, we will check the value at which Z is maximum and what is it and that will be our answer for part-1. For part-2, we will check for the minimum value and that will be our answer for part-2.

Complete step-by-step solution:
We will solve the first part of the question first.
Now, we have to maximize the value of $Z=3x+4y$, and the subject to constraints given to us are:
$x+y\le 4,x\ge 0,y\ge 0$
To solve this linear programming problem graphically, we will first have to draw the graph of the inequalities of the constraints.
To draw the graph of any given inequality, we first need to find any two solutions of the equation formed by replacing the inequality sign with the equal sign in the given inequality.
Now, the first inequality given to us is:
$x+y\le 4$
Hence, its equation will be:
$x+y=4$
Now, we need to obtain two solutions to this equation.
Sol-1: Let x=0
Thus, we get:
$\begin{aligned} & x+y=4 \\\ & \Rightarrow 0+y=4 \\\ & \Rightarrow y=4 \\\ \end{aligned}$
Hence, one solution is (0,4)
Sol-2: Let y=0
Thus, we get:
$\begin{aligned} & x+y=4 \\\ & \Rightarrow x+0=4 \\\ & \Rightarrow x=4 \\\ \end{aligned}$
Hence, the second solution is (4,0)
Thus, the two solutions to the equation $x+y=4$ are (0,4) and (4,0).
Now, the second inequality is $x\ge 0$
Hence, its equation will be:
$x=0$
Now, we know that this is the equation of the y-axis, so there is no need to find any solution to it. The required line is the y-axis.
Now, the third inequality is $y\ge 0$
Hence, its equation will be:
$y=0$
Now, we know that this is the equation of the x-axis, so there is no need to find any solution to it. The required line is the x-axis.
Hence, the graph made by these equations will look like this:

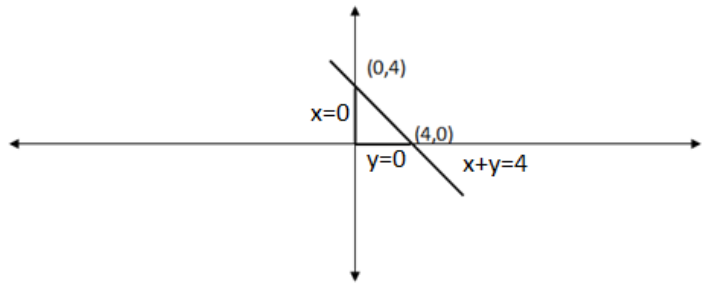
Now, we need to find the graph made by the inequalities.
We know that the graph of $x\ge 0$ and $y\ge 0$ is the complete first quadrant.
Thus, we only need to find which side of the line $x+y=4$ will give us our inequality $x+y\le 4$.
We know that any point which lies on the side of the line which contributes to the required inequality satisfies it too.
So let us take any point on the graph and put it into this inequality. If that point satisfies it, the side on which that point is lying will be our required side otherwise it will be the other side.
Let us take that point to be (0,0).
Putting this point into the inequality, we get:
$\begin{aligned} & x+y\le 4 \\\ & \Rightarrow 0+0\le 4 \\\ & \Rightarrow 0\le 4 \\\ \end{aligned}$
This inequality is correct, hence the point (0,0) satisfies this inequality and the side on which this point lies in the required side.
Thus, the required region of the graph is shown as:

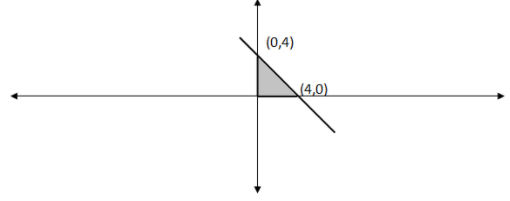
Thus, we get the corner points of the required region as (0,4), (4,0) and (0,0).
Now, we will one by one put these corner points into Z and see which will give us its maximum value.
Putting (0,4) into Z we get:
$\begin{aligned} & Z=3x+4y \\\ & \Rightarrow Z=3\left( 0 \right)+4\left( 4 \right) \\\ & \Rightarrow Z=0+16 \\\ & \Rightarrow Z=16 \\\ \end{aligned}$
Hence, we obtain Z=16 on putting (0,4) in it. .....(i)
Putting (4,0) into Z we get:
$\begin{aligned} & Z=3x+4y \\\ & \Rightarrow Z=3\left( 4 \right)+4\left( 0 \right) \\\ & \Rightarrow Z=12+0 \\\ & \Rightarrow Z=12 \\\ \end{aligned}$
Hence, we obtain Z=12 on putting (4,0) in it. .....(ii)
Putting (0,0) in Z we get:
$\begin{aligned} & Z=3x+4y \\\ & \Rightarrow Z=3\left( 0 \right)+4\left( 0 \right) \\\ & \Rightarrow Z=0+0 \\\ & \Rightarrow Z=0 \\\ \end{aligned}$
Thus, we get Z=0 on putting (0,0) in it. .....(iii)
Now, from (i), (ii) and (iii) we can see that the maximum value of Z is 16 at the point (0,4).
Hence, the maximum value of $Z=3x+4y$ is given as:
Z=16 at (0,4)
This is our required answer.
Now, like we solved the first part, we will solve the second question in the same way. But in the end, instead of looking for the maximum value, we will look for the minimum as the question has asked us to minimize the given constraint.
Now, the given constraint is:
$Z=-3x+4y$
The given subject to this constraint are:
$x+2y\le 8,3x+2y\le 12,x\ge 0,y\ge 0$
Now, as we did in the previous part, we will first find solutions to the corresponding equations of these inequalities.
The first inequality given to us is:
$x+2y\le 8$
Hence, its equation will be:
$x+2y=8$
Now, we will find its solutions.
Sol-1: let x=0
Thus, we get:
$\begin{aligned} & x+2y=8 \\\ & \Rightarrow 0+2y=8 \\\ & \Rightarrow 2y=8 \\\ & \Rightarrow y=\dfrac{8}{2}=4 \\\ \end{aligned}$
Hence, the first solution is (0,4).
Sol-2: Let y=0
Thus, we get:
$\begin{aligned} & x+2y=8 \\\ & \Rightarrow x+2\left( 0 \right)=8 \\\ & \Rightarrow x+0=8 \\\ & \Rightarrow x=8 \\\ \end{aligned}$
Hence, the second solution is (8,0)
Thus, the solutions to the equation $x+2y=8$ are (0,4) and (8,0).
Now, the second inequality given to us is:
$3x+2y\le 12$
Hence, its equation will be:
$3x+2y=12$
Now, we will find its solutions.
Sol-1: let x=0
Thus, we get:
$\begin{aligned} & 3x+2y=12 \\\ & \Rightarrow 3\left( 0 \right)+2y=12 \\\ & \Rightarrow 0+2y=12 \\\ & \Rightarrow 2y=12 \\\ & \Rightarrow y=\dfrac{12}{2}=6 \\\ \end{aligned}$
Hence, the first solution is (0,6).
Sol-2: let y=0
Thus, we get:
$\begin{aligned} & 3x+2y=12 \\\ & \Rightarrow 3x+2\left( 0 \right)=12 \\\ & \Rightarrow 3x+0=12 \\\ & \Rightarrow 3x=12 \\\ & \Rightarrow x=\dfrac{12}{3}=4 \\\ \end{aligned}$
Hence, the second solution is (4,0).
Thus, the solutions to the equation $3x+2y=12$ are (0,6) and (4,0).
Now the next two constraints are $x\ge 0$ and $y\ge 0$.
We have already established above that these two inequalities will give us the y-axis and the x-axis respectively.
Hence, the graph made by these equations will look like:

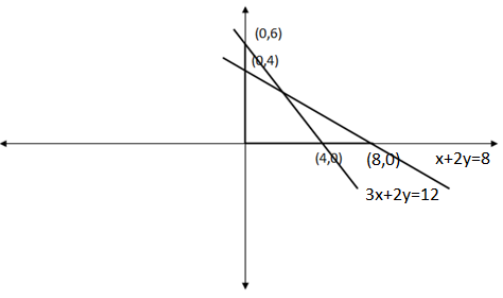
We can see from the graph that these two equations intersect at a point.
The coordinates of their point on intersection can be calculated by the elimination method as:
$\begin{aligned} & 3x+2y=12 \\\ & \underline{-\left( x+2y=8 \right)} \\\ & \underline{\text{ }2x=4\text{ }} \\\ & \Rightarrow 2x=4 \\\ & \Rightarrow x=2 \\\ \end{aligned}$
Putting this value of x in any of these two equations, we will get the corresponding value of y.
Putting x=2 in $x+2y=8$, we get:
$\begin{aligned} & x+2y=8 \\\ & \Rightarrow 2+2y=8 \\\ & \Rightarrow 2y=6 \\\ & \Rightarrow y=\dfrac{6}{2}=3 \\\ \end{aligned}$
Hence, the coordinates of the point of intersection are (2,3).
Now, as we did it in the first part, we will put (0,0) in both these inequalities to see which side of the line gives us our required inequality.
Putting (0,0) in the inequality $x+2y\le 8$ we get:
$\begin{aligned} & x+2y\le 8 \\\ & \Rightarrow 0+2\left( 0 \right)\le 8 \\\ & \Rightarrow 0+0\le 8 \\\ & \Rightarrow 0\le 8 \\\ \end{aligned}$
This inequality is correct. Hence, the side on which (0,0) will lie will be the required side of the inequality.
Now, putting the same point in the inequality $3x+2y\le 12$, we get:
$\begin{aligned} & 3x+2y\le 12 \\\ & \Rightarrow 3\left( 0 \right)+2\left( 0 \right)\le 12 \\\ & \Rightarrow 0+0\le 12 \\\ & \Rightarrow 0\le 12 \\\ \end{aligned}$
This inequality is also correct. Hence, the side on which (0,0) will lie will be the required side of the inequality.
Now, as mentioned above the inequalities $x\ge 0$ and $y\ge 0$ will give us the first quadrant.
Hence, the required region of the graph is given as:

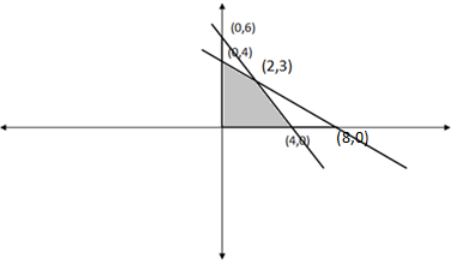
Now, we can see from the graph that the corner points are (0,4), (0,0), (4,0) and (2,3).
Now, we will one by one put these corner points into Z and see which will give us its minimum value.
Putting (0,4) into Z we get:

& Z=-3x+4y \\\ & \Rightarrow Z=-3\left( 0 \right)+4\left( 4 \right) \\\ & \Rightarrow Z=-0+16 \\\ & \Rightarrow Z=16 \\\ \end{aligned}$$ Thus, we get Z=16 from (0,4). .....(iv) Putting (0,0) into Z we get: $$\begin{aligned} & Z=-3x+4y \\\ & \Rightarrow Z=-3\left( 0 \right)+4\left( 0 \right) \\\ & \Rightarrow Z=-0+0 \\\ & \Rightarrow Z=0 \\\ \end{aligned}$$ Thus, we get Z=0 from (0,0). .....(v) Putting (4,0) into Z we get: $\begin{aligned} & Z=-3x+4y \\\ & \Rightarrow Z=-3\left( 4 \right)+4\left( 0 \right) \\\ & \Rightarrow Z=-12+0 \\\ & \Rightarrow Z=-12 \\\ \end{aligned}$ Hence, we get Z=-12 from (4,0). .....(vi) Putting (2,3) into Z we get: $\begin{aligned} & Z=-3x+4y \\\ & \Rightarrow Z=-3\left( 2 \right)+4\left( 3 \right) \\\ & \Rightarrow Z=-6+12 \\\ & \Rightarrow Z=6 \\\ \end{aligned}$ Hence, we get Z=6 from (2,3). .....(vii) Now, from (iv), (v), (vi) and (vii), we can see that the minimum value of Z is -12 which is obtained from (4,0). Hence, the minimum value of $Z=-3x+4y$ is given as: Z=-12 at (4,0) This is the required answer. **Note:** Here, we have mentioned the words ‘inequality’ and ‘equations’ a lot. It is important for us to know the difference between the two. When the LHS and the RHS are equal, i.e. when any two are equal, that representation is said to be the equation. When one of the two terms is smaller and the other is larger, i.e. the LHS and RHS are unequal, that representation is said to be the inequality.