Question

Solve the following linear programming problem graphically:
Minimise $Z = 200x + 500y$-------(1)
subject to the constraints:
$x + 2y \geqslant 10$------(2)
$3x + 4y \leqslant 24$-----(3)
$x \geqslant 0,y \geqslant 0$------(4)

Answer 1

To solve the given above question apply linear programming and consider the graph and plot using points obtained by the above equations such as (2), (3) in graph. Equation (4) is in the first quadrant which helps to find the points and substitute the resultant points in the equation (1) and we can find the minimum value.

Complete step by step solution:
Let us take
$Z = 200x + 500y$-------(1)
Now Consider equations
$x + 2y \geqslant 10$------(2)
$3x + 4y \leqslant 24$-----(3)
$x \geqslant 0,y \geqslant 0$------(4)
Now, consider equation (2)
$\Rightarrow \,\,x + 2y \geqslant 10$
Put $x = 0$ in equation (2), then
$\Rightarrow \,\,0 + 2y = 10$
$\Rightarrow \,\,2y = 10$
Divide both side by 2, then
$\Rightarrow \,\,y = \dfrac{{10}}{2}$
$\Rightarrow \,\,y = 5$
$\therefore$ we obtain a point $(x,y) = (0,5)$.
Put $y = 0$ in equation (2), then
$\Rightarrow \,\,x + 0 = 10$
$\Rightarrow \,\,x = 10$
$\therefore$ we obtain $(x,y) = (10,0)$
Now, Consider equation (3)
$\Rightarrow \,\,3x + 4y \leqslant 24$
Put $x = 0$in equation (3), then
$\Rightarrow \,\,0 + 4y = 24$
$\Rightarrow \,\,4y = 24$
Divide both side by 4, then
$\Rightarrow \,\,y = \dfrac{{24}}{4}$
$\Rightarrow \,\,y = 6$
$\therefore$ $(x,y) = (0,6)$
Put $y = 0$ in equation (3), then
$\Rightarrow \,\,3x + 4\left( 0 \right) = 24$
$\Rightarrow \,\,3x = 24$
Divide both side by 3, then
$\Rightarrow \,\,\,x = \dfrac{{24}}{3}$
$\Rightarrow \,\,\,x = 8$
$\therefore$ $(x,y) = (8,0)$
Now from equation (4) $x \geqslant 0,y \geqslant 0$
Equation (4) is in the first quadrant.
Plot the graph using all the obtained points from the above equation

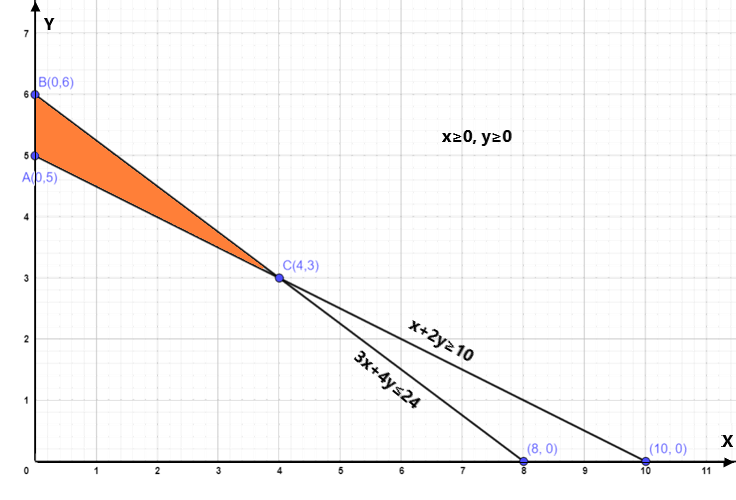
From the graph consider at point $A\left( {0,5} \right)$, $B\left( {0,6} \right)$ and to find the midpoint C consider the given equation (2) and (3)
$x + 2y = 10$
$3x + 4y = 24$
Now solve these equations by elimination method to obtain midpoint C
Multiply equation (a) by 3, then

$$\+ 3x + 6y = 30 \\\ \+ 3x + 4y = 24 \\\$$

Solve the equations by changing a sign, we get
$\Rightarrow \,\,2y = 6$
Divide 3 on both side, then
$\Rightarrow \,\,y = 3$
Now substitute value of y in equation (2) or (3), to get the value of x, then
Consider equation (2)
$\Rightarrow \,\,x + 2y = 10$
$\Rightarrow \,\,x + 2\left( 3 \right) = 10$
$\Rightarrow \,\,x + 6 = 10$
Subtract 6 on both side, then
$\Rightarrow \,\,x = 4$
Therefore, the midpoint C point is $C(4,3)$
The corner point of shaded region is $A\left( {0,5} \right)$, $B\left( {0,6} \right)$ and $C(4,3)$
Now, consider the equation (1)
$\Rightarrow \,\,Z = 200x + 500y$
At point $A\left( {0,5} \right)$, then
$\Rightarrow \,\,Z = 200\left( 0 \right) + 500\left( 5 \right)$
$\Rightarrow \,\,Z = 0 + 2500$
$\Rightarrow \,\,Z = 2500$
At point $B\left( {0,6} \right)$, then
$\Rightarrow \,\,Z = 200\left( 0 \right) + 500\left( 6 \right)$
$\Rightarrow \,\,Z = 0 + 3000$
$\Rightarrow \,\,Z = 3000$
Lastly, at point $C(4,3)$, then
$\Rightarrow \,\,Z = 200\left( 4 \right) + 500\left( 3 \right)$
$\Rightarrow \,\,Z = 800 + 1500$
$\Rightarrow \,\,Z = 2300$
Hence, the minimum value of $Z$ is $2300$ attained at the point $\left( {4,3} \right)$.

Note:
Linear programming is a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships. Linear programming is a technique for the optimization of a linear function subject to linear equality and linear inequality constraints. Linear equation is an equation between two variables that gives a straight line when plotted on a graph.