Question

Solve the following linear programming problem graphically:
Maximize $Z=7x+10y$ subject to constraints:
$\begin{aligned} & 4x+6y\le 240 \\\ & 6x+3y\le 240 \\\ & x\ge 10 \\\ & x\ge 0,y\ge 0 \\\ \end{aligned}$

Answer 1

First of all, we are going to draw the inequalities given as constraints on the graph paper and then from the region covered by the constraints take the corner points and then substitute these corner points in Z and see which point is giving you the maximum value. Then the point which is giving you the maximum value is the point at which Z is maximizing.

Complete step by step answer:
The constraints that we are subjected to:
$\begin{aligned} & 4x+6y\le 240 \\\ & 6x+3y\le 240 \\\ & x\ge 10 \\\ & x\ge 0,y\ge 0 \\\ \end{aligned}$
Using these constraints, we have to maximize$Z=7x+10y$.
In the below figure, we have drawn the constraints on the graph:

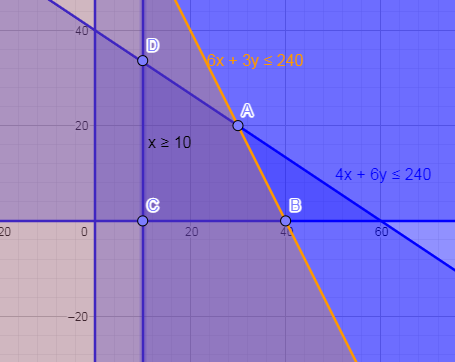
In the above figure, the region covered by ABCD is the intersection of all the constraints that have been given in the question $4x+6y\le 240,6x+3y\le 240,x\ge 10,x\ge 0,y\ge 0$. The coordinates of point A corresponds to$\left( 30,20 \right)$ and coordinates of point B correspond to (40, 0).
Now, we are going to substitute the value of points A and B in $Z=7x+10y$ we get,
Substituting the value of A (30, 20) in Z we get,
$\begin{aligned} & Z=7x+10y \\\ & \Rightarrow Z=7\left( 30 \right)+10\left( 20 \right) \\\ & \Rightarrow Z=210+200 \\\ & \Rightarrow Z=410 \\\ \end{aligned}$
Substituting the value of B(40, 0) in Z we get,
$\begin{aligned} & Z=7\left( 40 \right)+10\left( 0 \right) \\\ & \Rightarrow Z=280+0 \\\ & \Rightarrow Z=280 \\\ \end{aligned}$
From the above substitution of A and B in Z we have found that when substituting the point A in Z we have got the maximum value of Z i.e. 410.
Hence, Z is maximized at point A(30, 20) with the value of 410.

Note: You might think of how we are getting the point A while point B is obvious.
There are two ways in which you can get the point A:
First is to see from the graph, the intersection point of the equations$3x+5y=15\And 5x+2y=10$.
The other way is to solve the simultaneous equations $4x+6y=240;6x+3y=240$.
We are going to solve the simultaneous equations by elimination method.
$\begin{aligned} & 4x+6y=240..........Eq.(1) \\\ & 6x+3y=240..........Eq.(2) \\\ \end{aligned}$
Multiplying eq. (2) by 3 and subtracting this changed equation with eq.(1) and we get, $\begin{matrix} \left( 6x+3y=240 \right)\times 2 \\\ \dfrac{-\left( 4x+6y=240 \right)}{\left( 12-4 \right)x=240\left( 2-1 \right)} \\\ \end{matrix}$
Solving the above equation we get,
$8x=240$
Dividing 8 on both the sides of the above equation we get,
$x=\dfrac{240}{8}=30$
Substituting the above value of x in eq. (1) we get,
$\begin{aligned} & 4x+6y=240 \\\ & \Rightarrow 4\left( 30 \right)+6y=240 \\\ & \Rightarrow 120+6y=240 \\\ \end{aligned}$
Subtracting 120 on both the sides of the above equation we get,
$\begin{aligned} & 6y=240-120 \\\ & \Rightarrow 6y=120 \\\ & \Rightarrow y=\dfrac{120}{6} \\\ & \Rightarrow y=20 \\\ \end{aligned}$
Hence, we have got the point $A\left( 30,20 \right)$.