Question

Solve the following Linear Programming Problem graphically. Maximise profit ${\text{Z}} = {\text{Rs }}\left( {80{\text{x}} + 120{\text{y}}} \right)$
Subject to constraints are

$$9{\text{x}} + 12{\text{y}} \leqslant 180 \\\ 1{\text{x}} + 3{\text{y}} \leqslant {\text{30}} \\\ {\text{x}},{\text{y}} \geqslant {\text{0}} \\\$$

Answer 1

The linear programming is to find the maximum or minimum value of ${\text{z}}$ by converting the inequalities to equalities according to the given constraints. The intersecting point of the two equations is considered as corner points.

Complete step-by-step answer:
The given data in the question are,
${\text{Z}} = {\text{Rs }}\left( {80{\text{x}} + 120{\text{y}}} \right)$ is maximized under the following constraints,

$$9{\text{x}} + 12{\text{y}} \leqslant 180 \\\ 1{\text{x}} + 3{\text{y}} \leqslant {\text{30}} \\\ {\text{x}},{\text{y}} \geqslant {\text{0}} \\\$$

By converting the inequalities and equalities we get,

$$9{\text{x}} + 12{\text{y}} = 180\,......................(1) \\\ 1{\text{x}} + 3{\text{y}} = {\text{30 }}..........................{\text{(2)}} \\\$$

Step 1
While substituting ${\text{x}} = 0$ in the equation $(1)$ we get,
${\text{12y}} = 180$
By solving we get,
${\text{y}} = \dfrac{{180}}{{12}}$
By dividing the above we get,
${\text{y}} = 15$
From the equation $(1)$ , while substituting ${\text{x}} = 0$ we get the points as $(0,15)$
While substituting ${\text{y}} = 0$ in the equation $(1)$ we get,
${\text{9x}} = 180$
By solving we get,
${\text{x}} = \dfrac{{180}}{9}$
By dividing the above we get,
${\text{x}} = 20$
From the equation $(1)$ , while substituting ${\text{y}} = 0$ we get the points as $(20,0)$
While substituting ${\text{x}} = 0$ in the equation $(2)$ we get,
${\text{3y}} = 30$
By solving we get,
${\text{y}} = \dfrac{{30}}{3}$
By dividing the above we get,
${\text{y}} = 10$
From the equation $(2)$ , while substituting ${\text{x}} = 0$ we get the points as $(0,10)$
While substituting ${\text{y}} = 0$ in the equation $(2)$ we get,
${\text{x}} = 30$
From the equation $(2)$ , while substituting ${\text{y}} = 0$ we get the points as $(30,0)$

Step 2
By plotting all the above points in a graph we get the graph as,

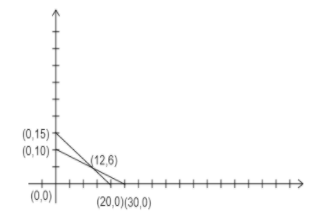
The two lines intersect at $(12,6)$ and the other corner points of the region are $(0,10),(0,0)\,{\text{and }}(20,0)$ .

Step 3
To find the maximum profit of ${\text{z}}$ , we have to find all values of ${\text{z}}$ in the corner points,
${\text{Z}} = {\text{Rs }}\left( {80{\text{x}} + 120{\text{y}}} \right)$
When we substitute $(0,10)$ in the above equation we get,
${\text{Z}} = 0 + 120(10)$
By solving the above we get,
${\text{Z}} = 1200.....................({\text{i)}}$
When we substitute $(0,0)$ we get,
${\text{Z}} = 0\,.........................({\text{ii}})$
When we substitute $(20,0)$ we get,
${\text{Z}} = 80(20) + 0$
By solving we get,
${\text{Z}} = 1600\,..................({\text{iii}})$
When we substitute $(12,6)$ we get,
${\text{Z}} = 80(12) + 120(6)$
By simplifying we get,
${\text{Z}} = 960 + 720$
By solving we get,
${\text{Z}} = 1680\,..................({\text{iv)}}$
The maximum value of $({\text{i),(ii),(iii) and (iv)}}$ is $({\text{iv)}}$ .
Hence, ${\text{Z}}$ is maximum at $(12,6)$ and the maximum value is $1680$ .
Therefore, the maximum profit is ${\text{Rs}}.1680$

Note: There are three types of linear programming. We have to solve the problem according to the question. In the constraints given we have to note that the value of x and y should be greater than or equal to $0$