Question

Solve the following equations:

14. $|||x-2|-2|-2|=2$
15. $|4x+3|+|3x-4|=12$
16. Solve $|x^2-2x+8|=8$

Answer 1

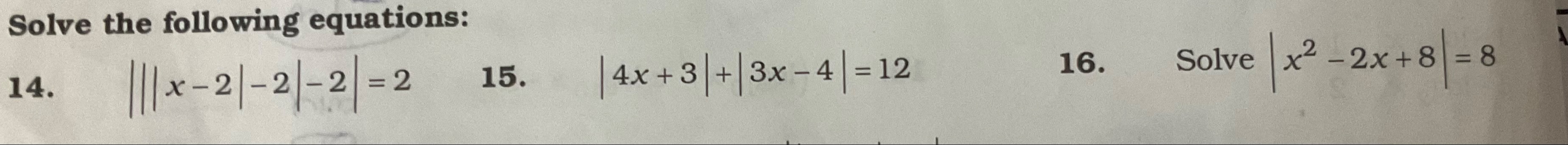
x = -4, 0, 4, 8; x = -11/7, 13/7; x = 0, 2

Answer 2

Here are the solutions to the given equations.

14. $|||x-2|-2|-2|=2$

Explanation: We solve the equation by peeling off the absolute values layer by layer. $|||x-2|-2|-2|=2$ implies $||x-2|-2|-2 = 2$ or $||x-2|-2|-2 = -2$.

Case 1: $||x-2|-2|-2 = 2$ $||x-2|-2| = 4$ This implies $|x-2|-2 = 4$ or $|x-2|-2 = -4$. Subcase 1.1: $|x-2|-2 = 4$ $|x-2| = 6$ This implies $x-2 = 6$ or $x-2 = -6$. $x = 8$ or $x = -4$. Subcase 1.2: $|x-2|-2 = -4$ $|x-2| = -2$ Since the absolute value cannot be negative, there are no real solutions in this subcase.

Case 2: $||x-2|-2|-2 = -2$ $||x-2|-2| = 0$ This implies $|x-2|-2 = 0$. $|x-2| = 2$ This implies $x-2 = 2$ or $x-2 = -2$. $x = 4$ or $x = 0$.

Combining all solutions from Case 1 and Case 2, the solutions are $x \in \{-4, 0, 4, 8\}$.

15. $|4x+3|+|3x-4|=12$

Explanation: We identify the critical points where the expressions inside the absolute values change sign. These are $4x+3=0 \implies x = -3/4$ and $3x-4=0 \implies x = 4/3$. These points divide the number line into three intervals: $(-\infty, -3/4)$, $[-3/4, 4/3)$, and $[4/3, \infty)$. We solve the equation in each interval.

Interval 1: $x < -3/4$ In this interval, $4x+3 < 0$ and $3x-4 < 0$. So, $|4x+3| = -(4x+3)$ and $|3x-4| = -(3x-4)$. The equation becomes: $-(4x+3) - (3x-4) = 12$ $-4x - 3 - 3x + 4 = 12$ $-7x + 1 = 12$ $-7x = 11$ $x = -11/7$. Since $-11/7 \approx -1.57$ and $-3/4 = -0.75$, $x = -11/7$ is in the interval $(-\infty, -3/4)$. This is a valid solution.

Interval 2: $-3/4 \le x < 4/3$ In this interval, $4x+3 \ge 0$ and $3x-4 < 0$. So, $|4x+3| = 4x+3$ and $|3x-4| = -(3x-4)$. The equation becomes: $(4x+3) - (3x-4) = 12$ $4x + 3 - 3x + 4 = 12$ $x + 7 = 12$ $x = 5$. Since $4/3 \approx 1.33$, $x = 5$ is not in the interval $[-3/4, 4/3)$. This is not a valid solution.

Interval 3: $x \ge 4/3$ In this interval, $4x+3 \ge 0$ and $3x-4 \ge 0$. So, $|4x+3| = 4x+3$ and $|3x-4| = 3x-4$. The equation becomes: $(4x+3) + (3x-4) = 12$ $4x + 3 + 3x - 4 = 12$ $7x - 1 = 12$ $7x = 13$ $x = 13/7$. Since $13/7 \approx 1.86$ and $4/3 \approx 1.33$, $x = 13/7$ is in the interval $[4/3, \infty)$. This is a valid solution.

Combining all valid solutions, the solutions are $x \in \{-11/7, 13/7\}$.

16. $|x^2-2x+8|=8$

Explanation: We solve the equation by considering the two cases for the expression inside the absolute value. $|x^2-2x+8|=8$ implies $x^2-2x+8 = 8$ or $x^2-2x+8 = -8$.

Case 1: $x^2-2x+8 = 8$ $x^2 - 2x = 0$ Factor out $x$: $x(x-2) = 0$ This gives $x = 0$ or $x = 2$.

Case 2: $x^2-2x+8 = -8$ $x^2 - 2x + 16 = 0$ We check the discriminant of this quadratic equation, $\Delta = b^2 - 4ac$. Here $a=1, b=-2, c=16$. $\Delta = (-2)^2 - 4(1)(16) = 4 - 64 = -60$. Since the discriminant is negative ($\Delta < 0$), the quadratic equation has no real roots.

Combining all real solutions from Case 1 and Case 2, the solutions are $x \in \{0, 2\}$.