Question

Solve the following equation for x:

$\frac{6}{5}log_a x.log_{10} a.log_a 5 - 3log_{10}(\frac{x}{10}) = log_{100} x + log_4 2$

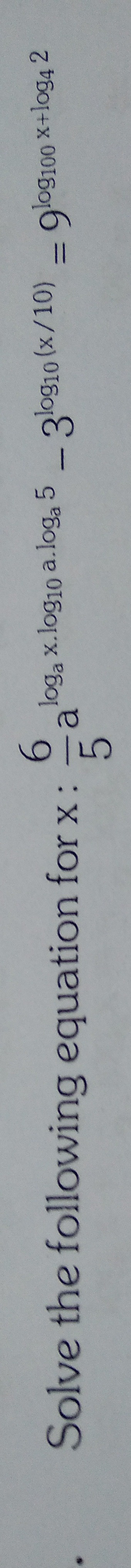
Answer 1

The solution to the equation is $x = 10^{25/23}$.

Answer 2

The equation is simplified by converting all logarithms to base 10. The term $log_a x \cdot log_{10} a \cdot log_a 5$ is simplified to $\frac{6}{5} log_{10} x$ by assuming $a=5$, which is a natural choice given the structure of the equation and the requirement for a unique solution for $x$. The other terms are simplified using standard logarithm properties. The equation is then rewritten in terms of $Y = log_{10} x$, leading to a linear equation in $Y$. Solving for $Y$ gives $log_{10} x = \frac{25}{23}$, from which $x = 10^{25/23}$ is obtained.