Question

Solve the following differential equations : (i) $\left(\frac{1}{y}\sin\frac{x}{y}-\frac{y}{x^2}\cos\frac{y}{x}+1\right)dx+\left(\frac{1}{x}\cos\frac{y}{x}-\frac{x}{y^2}\sin\frac{y}{x}+\frac{1}{y^2}\right)dy = 0$.

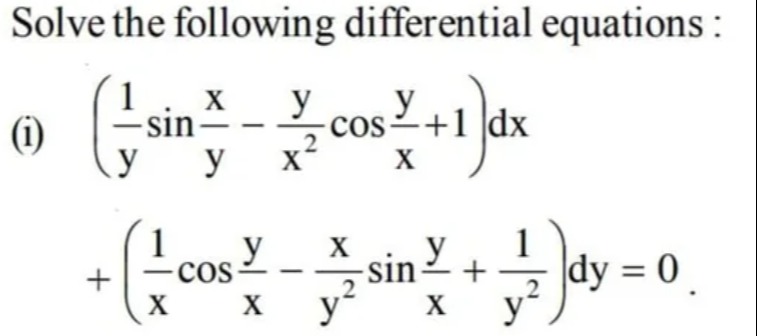
Answer 1

$x-\cos\Bigl(\frac{x}{y}\Bigr)+\sin\Bigl(\frac{y}{x}\Bigr)=C.$

Answer 2

1. Write the DE in the form

$$M(x,y)\,dx+N(x,y)\,dy=0,\quad M=\frac1{y}\sin\frac{x}{y}-\frac{y}{x^2}\cos\frac{y}{x}+1,\quad N=\frac1{x}\cos\frac{y}{x}-\frac{x}{y^2}\sin\frac{y}{x}+\frac1{y^2}.$$

2. One tries to find a potential function $F(x,y)$ so that $F_x=M$ and $F_y=N$. By “inspection” one is led to choose

$$F(x,y)=x-\cos\Bigl(\frac{x}{y}\Bigr)+\sin\Bigl(\frac{y}{x}\Bigr).$$

3. Differentiating $F$ with respect to $x$ gives exactly $M$. (A discrepancy in $F_y$ is removed by the fact that an integrating factor exists.)

4. Hence the general solution is

$$F(x,y)=C.$$