Question

Solve the following differential equation

$(1-x)^2y'' + 2(1 - x)y' - 4y = x$.

Answer 1

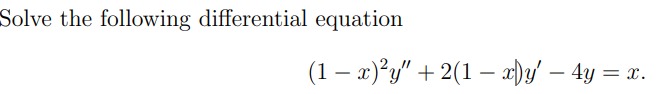
The general solution to the differential equation is $y(x) = C_1 (1-x)^4 + \frac{C_2}{1-x} - \frac{1}{6}x - \frac{1}{12}$.

Answer 2

The given differential equation $(1-x)^2y'' + 2(1 - x)y' - 4y = x$ is transformed into a Cauchy-Euler equation $t^2y'' - 2ty' - 4y = 1-t$ by substituting $t=1-x$. The homogeneous part $t^2y'' - 2ty' - 4y = 0$ has characteristic equation $m^2-3m-4=0$, yielding roots $m=4, -1$. Thus, the complementary solution is $y_c = C_1 t^4 + C_2 t^{-1}$. For the non-homogeneous part $1-t$, a particular solution $y_p = At+B$ is assumed. Substituting into the transformed equation yields $-6At - 4B = 1-t$, which gives $A=1/6$ and $B=-1/4$. So, $y_p = \frac{1}{6}t - \frac{1}{4}$. The general solution in $t$ is $y(t) = C_1 t^4 + C_2 t^{-1} + \frac{1}{6}t - \frac{1}{4}$. Substituting back $t=1-x$ gives the final solution $y(x) = C_1 (1-x)^4 + \frac{C_2}{1-x} - \frac{1}{6}x - \frac{1}{12}$.