Solveeit Logo
Login

Question

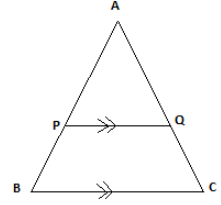
Question: Solve the following: A \((\triangle ABC)\; =\; 360\; cm^2\) A \((\square BPQC)\; =\; 110\; cm^2\...

Solve the following:
A (△ABC)  =  360  cm2(\triangle ABC)\; =\; 360\; cm^2
A (□BPQC)  =  110  cm2(\square BPQC)\; =\; 110\; cm^2
AP = 10 cm
Then find AQQC\dfrac{{AQ}}{{QC}}

Explanation

Solution

Use the Triangle Proportionality Theorem, which states that if a line is parallel to one side of the triangle and it intersects with the other two sides, then that side is divided proportionally. If two triangles have two pairs of sides in the same ratio and the included angles are equal, then the triangles are similar.
If the triangles are similar, then the angles of the pairs of the corresponding angles are the same. Also, their corresponding pairs of the side are in the same proportion. Similar triangles have the same shape but do not have the same size.

Complete step by step solution:
In the given figure


PQ is parallel to BC, hence by using parallel line theorem, we can say
∠APQ=∠ABC\angle APQ = \angle ABC
∠AQP=∠ACB\angle AQP = \angle ACB
∠A\angle A is common in both the triangle; hence we can say both the triangles are similar
Given the area
A (△ABC)  =  360  cm2(\triangle ABC)\; =\; 360\; cm^2
A (□BPQC)  =  110  cm2(\square BPQC)\; =\; 110\; cm^2
And as the △APQ\vartriangle APQ and △ABC\vartriangle ABC are similar so we can write the area of the triangles will also be in the same proportion
△ABC△APQ=ABAP\dfrac{{\vartriangle ABC}}{{\vartriangle APQ}} = \dfrac{{AB}}{{AP}}
Where the area △APQ\vartriangle APQ can be written as the difference of area of △ABC\vartriangle ABC and the area of a trapezoid □BPQC\square BPQC
Now substituting the values, we can write

⇒360360−110=(ABAP)2 ⇒360250=(ABAP)2 ⇒ABAP=3625 ⇒65 \Rightarrow\dfrac{{360}}{{360 - 110}} = {\left( {\dfrac{{AB}}{{AP}}} \right)^2} \\\ \Rightarrow\dfrac{{360}}{{250}} = {\left( {\dfrac{{AB}}{{AP}}} \right)^2} \\\ \Rightarrow\dfrac{{AB}}{{AP}} = \sqrt {\dfrac{{36}}{{25}}} \\\ \Rightarrow\dfrac{6}{5} \\\

Hence the ratio of the length of the side ABAP=65\dfrac{{AB}}{{AP}} = \dfrac{6}{5}
Since length of AP=10cmAP = 10cm
Hence we can write

AB=65×AP ⇒65×10 ⇒12cm AB = \dfrac{6}{5} \times AP \\\ \Rightarrow\dfrac{6}{5} \times 10 \\\ \Rightarrow12cm \\\

Since length of PB=AB−APPB = AB - AP
Hence, PB=12−10=2cmPB = 12 - 10 = 2cm
Triangle Proportionality Theorem which states that if a line is parallel to one side of the triangle and it intersects with the other two sides, we can say
APPB=AQQC\dfrac{{AP}}{{PB}} = \dfrac{{AQ}}{{QC}}
Hence by substituting the values
APPB=AQQC=122=6\dfrac{{AP}}{{PB}} = \dfrac{{AQ}}{{QC}} = \dfrac{{12}}{2} = 6
We get, AQQC=6\dfrac{{AQ}}{{QC}} = 6

Note: To prove two triangles to be similar, students must check whether all the angles are equal and/or, the corresponding pairs of sides are in the same ratio. Students should not get confused with the area of the quadrilateral given in the question; it is actually given as so that the area of both the triangles can be determined.