Question

Solve the equations using graphical method: $2x - y = 2$ and $- 4x - y = - 4$
A. $\left( {1, - 1} \right)$
B. $\left( {1,0} \right)$
C. $\left( {2, - 1} \right)$
D. $\left( {0,1} \right)$

Answer 1

In this question, we have been given two equations. We have to solve these two equations using graphical methods. What this means is that we have to plot the two lines representing the two equations on the same graph, see where they are meeting (or we can say intersecting), find the coordinates of the point and then, we are going to arrive at our answer. To simplify the problem, we can remove the negative signs from both of the sides of the second equation, so that after doing that, we are only dealing with the two equations whose x coordinates (or we can say abscissa) have the same sign. This helps in making the equations look cleaner and thus, prevents the confusion from occurring.

Complete step-by-step answer:
The given equations are $2x - y = 2$ and $- 4x - y = - 4$.
We are first going to clean up the second equation so as to make the work look cleaner and it will help from making an error by preventing confusion.
So, $- 4x - y = - 4$ becomes $4x + y = 4$
Let us first take the first equation, $2x - y = 2$
Putting $x = 1$ and $x = 2$, we have:
$y = 0$ and $y = 2$
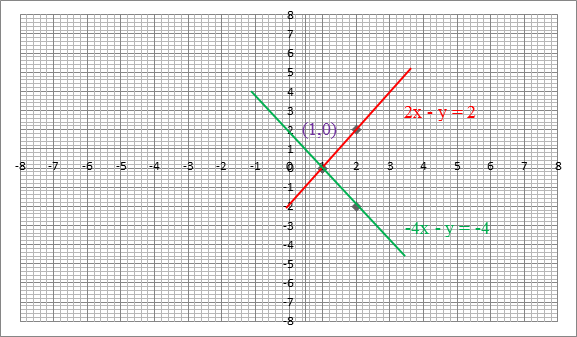
Now, plotting $\left( {1,0} \right)$ and $\left( {2,2} \right)$, joining them, we get a straight line.
Now, taking the second equation $4x + y = 4$
Putting $x = 1$ and $x = 2$, we have:
$y = 0$ and $y = - 2$
Now, plotting $\left( {1,0} \right)$ and $\left( {2, - 2} \right)$, joining them, we get a straight line.
Now, these two lines intersect at $\left( {1,0} \right)$, and this is our solution.

Hence, the correct option is B).

Note: So, we saw that in solving questions like these, we first write what has been given to us. Then, we clean the equations up if possible (like removing the common negative sign), bring any of the given equations to the lowest form if possible (by dividing both the sides of the equation by a common factor) so that we end up dealing with the smallest equation possible and so that we do not have to extend the line of the other equation on the graph too much. This greatly helps in preventing the confusion from occurring.