Question

Solve the equations $3x + 2y = 5$ and $2x - 3y = 7$ graphically.

Answer 1

: Linear equations in two variables are straight lines when they are plotted on a graph. And, if two straight lines intersect at a point, then the point gives us the solution for the equations. We use this concept to solve this problem. We will also know about some rules that have to be followed to find the consistency and nature of solutions.

Complete step by step solution:
If we have two equations, say ${a_1}x + {b_1}y + {c_1} = 0$ and ${a_2}x + {b_2}y + {c_2} = 0$ , then these two equations are –
Consistent and have unique solution if $\dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}$ , and the two straight lines represented by these two equations are intersecting.
Consistent and have infinitely many solutions if $\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} = \dfrac{{{c_1}}}{{{c_2}}}$ , and the two lines are coinciding lines.
Inconsistent and have no solution if $\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}$ , and the two lines are parallel.
So, in the question, $\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{3}{2}$ and $\dfrac{{{b_1}}}{{{b_2}}} = - \dfrac{2}{3}$ . So, here, $\dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}$ which means, the equations have a unique solution.
To draw a graph for an equation $ax + by + c = 0$ , we need to follow these steps-
First of all, consider the value of $x$ to be zero, and calculate the value of $y$ by substituting $x = 0$ in the equation, and you will get one of the points on line as $(0,{y_{{\text{at }}x = 0}})$ .
Now, consider, the value of $y$ to be zero, and calculate the value of $x$ by substituting $y = 0$ in the equation, and you will get another point on line as $({x_{{\text{at }}y = 0}},0)$ .
Now, join these two points, and you will get the graph for this equation.
Similarly, draw the graph for another equation also, and find the solution accordingly.
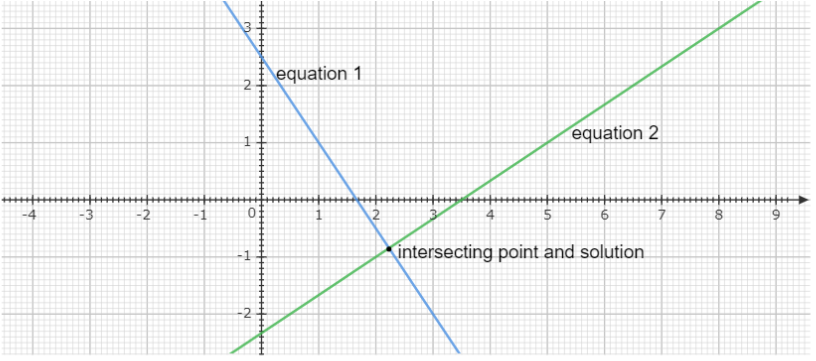
Here, in the equation $3x + 2y = 5$ , if $x = 0$ , we get $y = \dfrac{5}{2}$ , so one point is $\left( {0,\dfrac{5}{2}} \right)$ .
If $y = 0$ , we get $x = \dfrac{5}{3}$ so, the point is $\left( {\dfrac{5}{3},0} \right)$ . Join these two points to get a straight line.
And in the equation, $2x - 3y = 7$ , if $x = 0$ , we get $y = - \dfrac{7}{3}$ , so the point is $\left( {0, - \dfrac{7}{3}} \right)$ and if $y = 0$ , we get $x = \dfrac{7}{2}$ , so the point is $\left( {\dfrac{7}{2},0} \right)$ . Join these two points to get another straight line.
These two straight lines meet at a point $\left( {\dfrac{{29}}{{13}}, - \dfrac{{11}}{{13}}} \right)$ .

Note:
A linear equation in two variables is always a straight line. Before solving any question, make sure that you check the consistency and also the nature of the solution. And be careful while taking the points. If we consider $x = 0$ , that means that we are finding the intersection point of the given line and the Y-axis. And similarly, if we consider $y = 0$ , that means that we are finding the intersection point of the given line and the X-axis.