Question

Solve the equation $(x-1)^4 + (x-5)^4 = 82$.

Answer 1

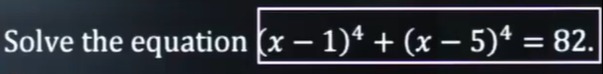
The solutions are $x = 2, 4, 3+5i, 3-5i$.

Answer 2

The given equation is $(x-1)^4 + (x-5)^4 = 82$.

To simplify this equation, we can use a substitution. Notice that the terms are $(x-1)$ and $(x-5)$. The average of these two terms is $\frac{(x-1) + (x-5)}{2} = \frac{2x-6}{2} = x-3$. Let $y = x-3$. Then, we can express $(x-1)$ and $(x-5)$ in terms of $y$: $x-1 = (x-3) + 2 = y+2$ $x-5 = (x-3) - 2 = y-2$

Substitute these into the original equation: $(y+2)^4 + (y-2)^4 = 82$

We can expand the terms using the binomial theorem or the identity $(a+b)^4 + (a-b)^4 = 2(a^4 + 6a^2b^2 + b^4)$. Using the identity with $a=y$ and $b=2$: $2(y^4 + 6y^2(2^2) + 2^4) = 82$ $2(y^4 + 6y^2(4) + 16) = 82$ $2(y^4 + 24y^2 + 16) = 82$

Divide both sides by 2: $y^4 + 24y^2 + 16 = 41$

Rearrange the equation to form a quadratic equation in terms of $y^2$: $y^4 + 24y^2 + 16 - 41 = 0$ $y^4 + 24y^2 - 25 = 0$

Let $z = y^2$. Substituting $z$ into the equation gives a quadratic equation: $z^2 + 24z - 25 = 0$

We can solve this quadratic equation by factoring. We need two numbers that multiply to -25 and add to 24. These numbers are 25 and -1. $(z+25)(z-1) = 0$

This gives two possible values for $z$:

1. $z+25 = 0 \implies z = -25$
2. $z-1 = 0 \implies z = 1$

Now, substitute back $z = y^2$:

Case 1: $y^2 = -25$ Taking the square root of both sides: $y = \pm\sqrt{-25} = \pm 5i$

Case 2: $y^2 = 1$ Taking the square root of both sides: $y = \pm\sqrt{1} = \pm 1$

Finally, substitute back $y = x-3$ to find the values of $x$:

From Case 1 ($y = \pm 5i$): If $y = 5i$: $x-3 = 5i$ $x = 3 + 5i$

If $y = -5i$: $x-3 = -5i$ $x = 3 - 5i$

From Case 2 ($y = \pm 1$): If $y = 1$: $x-3 = 1$ $x = 1+3$ $x = 4$

If $y = -1$: $x-3 = -1$ $x = -1+3$ $x = 2$

Thus, the solutions to the equation are $x=2, x=4, x=3+5i,$ and $x=3-5i$.

The real solutions are $x=2$ and $x=4$. The complex solutions are $x=3+5i$ and $x=3-5i$.

The question does not specify if the solutions should be real or complex, so all four roots of the quartic equation are valid solutions.

Explanation of the solution:

1. Substitution: Let $y = x-3$ to simplify the bases $(x-1)$ and $(x-5)$ into $(y+2)$ and $(y-2)$ respectively.
2. Expansion: Use the identity $(a+b)^4 + (a-b)^4 = 2(a^4 + 6a^2b^2 + b^4)$ with $a=y$ and $b=2$ to expand the left side of the equation, resulting in $2(y^4 + 24y^2 + 16) = 82$.
3. Simplification: Divide by 2 and rearrange to get a quadratic equation in terms of $y^2$: $y^4 + 24y^2 - 25 = 0$.
4. Solve for $y^2$: Let $z = y^2$. The equation becomes $z^2 + 24z - 25 = 0$. Factor this quadratic as $(z+25)(z-1) = 0$, yielding $z = -25$ or $z = 1$.
5. Solve for $y$: Substitute back $y^2$ for $z$.
   • If $y^2 = -25$, then $y = \pm 5i$.
   • If $y^2 = 1$, then $y = \pm 1$.
6. Solve for $x$: Substitute back $y = x-3$ for each value of $y$ to find the corresponding $x$ values: $x = 3 \pm 5i$ and $x = 2, 4$.