Question
Question: Solve $\tan 2x = -\cot(x + \frac{\pi}{3})$...
Solve tan2x=−cot(x+3π)
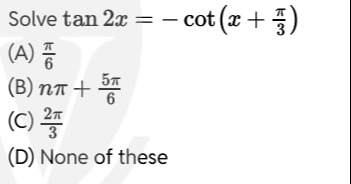
A
6π
B
nπ+65π
C
32π
D
None of these
Answer
nπ+65π
Explanation
Solution
Use the identity −cotθ=tan(2π+θ) to rewrite the equation as tan2x=tan(x+65π). The general solution for tanA=tanB is A=nπ+B. Applying this, 2x=nπ+x+65π, which simplifies to x=nπ+65π. This matches option (B).
