Question

Solve: $\sin \left( {{\tan }^{-1}}x \right),\left| x \right|<1$ is equal to
A. $\dfrac{x}{\sqrt{1-{{x}^{2}}}}$
B. $\dfrac{1}{\sqrt{1-{{x}^{2}}}}$
C. $\dfrac{1}{\sqrt{1+{{x}^{2}}}}$
D. $\dfrac{x}{\sqrt{1+{{x}^{2}}}}$

Answer 1

Hint : To solve the question, we need to assume that the value of ${{\tan }^{-1}}x$ is $\text{ }\\!\\!\theta\\!\\!\text{ }$ and then place the value in place of ${{\tan }^{-1}}x$ to find the value of $\sin \text{ }\\!\\!\theta\\!\\!\text{ }$ and remove $\text{ }\\!\\!\theta\\!\\!\text{ }$ by the trigonometric value of ${{\tan }^{-1}}x$ . The formula for $\tan \text{ }\\!\\!\theta\\!\\!\text{ }$ is
$\tan \text{ }\\!\\!\theta\\!\\!\text{ }=\dfrac{\text{height}}{\text{base}}$ of an assumed triangle and then find the value of $\text{ }\\!\\!\theta\\!\\!\text{ }$ and place it with $\sin \text{ }\\!\\!\theta\\!\\!\text{ }$ to find the value of $\sin \text{ }\\!\\!\theta\\!\\!\text{ }$ in terms of $x$ .

Complete step-by-step answer :
Let us first draw a triangle based on the question with $\text{ }\\!\\!\theta\\!\\!\text{ }$ as angle at point A.

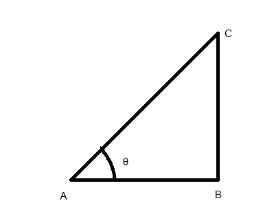
where ${{\tan }^{-1}}x$ which means if we equate the value of $x$ in terms of $\text{ }\\!\\!\theta\\!\\!\text{ }$ , we get the value of $x$ as:
$\Rightarrow {{\tan }^{-1}}x=\text{ }\\!\\!\theta\\!\\!\text{ }$
$\Rightarrow x=\tan \text{ }\\!\\!\theta\\!\\!\text{ }$
Now according to the trigonometric formula, the value of the $\text{tangent}$ is given as:
$\tan \text{ }\\!\\!\theta\\!\\!\text{ }=\dfrac{\text{height}}{\text{base}}$
Equating the value of $\tan \text{ }\\!\\!\theta\\!\\!\text{ }=x$ with $\tan \text{ }\\!\\!\theta\\!\\!\text{ }=\dfrac{\text{height}}{\text{base}}$ , we get the value of the ratio of $\dfrac{\text{height}}{\text{base}}$ as $\dfrac{x}{1}$ .
Therefore, we can say that the height of the triangle is $x$ and the base is $1$ . Using Pythagoras theorem we can find the value of the hypotenuse of the triangle as:
Hypotenuse $=\sqrt{\text{heigh}{{\text{t}}^{2}}+\text{bas}{{\text{e}}^{2}}}$
$\Rightarrow \sqrt{{{x}^{2}}+{{\text{1}}^{2}}}$
Now as we have all the values i.e. height, base and hypotenuse we can find the value of $\sin \left( {{\tan }^{-1}}x \right)$ by replacing it with $\sin \text{ }\\!\\!\theta\\!\\!\text{ }$ and after that we find the value of $\sin \text{ }\\!\\!\theta\\!\\!\text{ }$ as:
$\sin \text{ }\\!\\!\theta\\!\\!\text{ }=\dfrac{\text{height}}{\text{hypotenuse}}$
Placing the values of height and hypotenuse in the above formula, we get the value of $\sin \text{ }\\!\\!\theta\\!\\!\text{ }$ as:
$\Rightarrow \sin \text{ }\\!\\!\theta\\!\\!\text{ }=\dfrac{x}{\sqrt{{{x}^{2}}+1}}$
Now on the L.H.S, the value of $\sin \text{ }\\!\\!\theta\\!\\!\text{ }$ can be replaced by $\sin \left( {{\tan }^{-1}}x \right)$ with ${{\tan }^{-1}}x=\text{ }\\!\\!\theta\\!\\!\text{ }$ . Hence, the value of $\sin \left( {{\tan }^{-1}}x \right)$ is $\dfrac{x}{\sqrt{{{x}^{2}}+1}}$ .
So, the correct answer is “ $\dfrac{x}{\sqrt{{{x}^{2}}+1}}$ ”.

Note : Student may make mistake as the value of inverse is such as ${{\tan }^{-1}}x=\dfrac{1}{\tan x}$ , but ${{\left( \tan x \right)}^{-1}}=\dfrac{1}{\tan x}$ . Hence such mistakes should be avoided and the angle should be taken in any one point of the triangle like A for both $\tan \text{ }\\!\\!\theta\\!\\!\text{ }$ and $\sin \text{ }\\!\\!\theta\\!\\!\text{ }$ .