Question

Solve: $\frac{(x^2+4x-12)(x^2-x-20)}{(6x-x^2-5)(x^2+2x-8)} \leq 0$

Answer 1

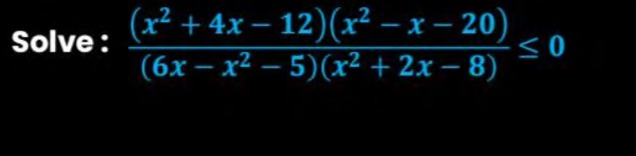
(-\infty, -6] \cup (5, \infty)

Answer 2

To solve the inequality $\frac{(x^2+4x-12)(x^2-x-20)}{(6x-x^2-5)(x^2+2x-8)} \leq 0$, we first factorize each quadratic expression.

1. Factorize the numerator:

   • $x^2+4x-12 = (x+6)(x-2)$
   • $x^2-x-20 = (x-5)(x+4)$ The numerator is $(x+6)(x-2)(x-5)(x+4)$. The roots of the numerator are $x = -6, 2, 5, -4$.

2. Factorize the denominator:

   • $6x-x^2-5 = -(x^2-6x+5) = -(x-1)(x-5)$
   • $x^2+2x-8 = (x+4)(x-2)$ The denominator is $-(x-1)(x-5)(x+4)(x-2)$. The roots of the denominator are $x = 1, 5, -4, 2$. These values must be excluded from the solution set as they make the denominator zero.

The inequality becomes: $\frac{(x+6)(x-2)(x-5)(x+4)}{-(x-1)(x-5)(x+4)(x-2)} \leq 0$

The critical points from the numerator and denominator are $-6, -4, 1, 2, 5$. These points divide the number line into intervals. We will analyze the sign of the expression in each interval.

Let $N(x) = (x+6)(x+4)(x-2)(x-5)$ and $D(x) = -(x-1)(x-5)(x+4)(x-2)$. We need to find where $E(x) = \frac{N(x)}{D(x)} \leq 0$.

Sign analysis for $N(x)$: The roots are $-6, -4, 2, 5$.

• For $x < -6$: $N(x)$ is positive.
• For $-6 < x < -4$: $N(x)$ is negative.
• For $-4 < x < 2$: $N(x)$ is positive.
• For $2 < x < 5$: $N(x)$ is negative.
• For $x > 5$: $N(x)$ is positive.

Sign analysis for $D(x)$: The roots are $-4, 1, 2, 5$.

• For $x < -4$: $D(x)$ is negative.
• For $-4 < x < 1$: $D(x)$ is positive.
• For $1 < x < 2$: $D(x)$ is positive.
• For $2 < x < 5$: $D(x)$ is negative.
• For $x > 5$: $D(x)$ is negative.

Now, we combine the signs to find the sign of $E(x) = \frac{N(x)}{D(x)}$:

Interval	$N(x)$ Sign	$D(x)$ Sign	$E(x)$ Sign	$E(x) \leq 0$?
$x < -6$	$+$	$-$	$-$	Yes
$-6 < x < -4$	$-$	$-$	$+$	No
$-4 < x < 1$	$+$	$+$	$+$	No
$1 < x < 2$	$+$	$+$	$+$	No
$2 < x < 5$	$-$	$-$	$+$	No
$x > 5$	$+$	$-$	$-$	Yes

The inequality $E(x) \leq 0$ holds for $x \in (-\infty, -6]$ and $x \in (5, \infty)$. We must also consider the points where the numerator is zero, which are $x = -6, -4, 2, 5$.

• $x = -6$: $N(x)=0$, $D(x) \neq 0$. So $E(x)=0$. This point is included.
• $x = -4$: $D(x)=0$. This point is excluded.
• $x = 2$: $D(x)=0$. This point is excluded.
• $x = 5$: $D(x)=0$. This point is excluded.

The points where the denominator is zero are $x = 1, 5, -4, 2$. These must always be excluded.

Combining the intervals where $E(x) < 0$ and the points where $E(x) = 0$ (and the denominator is non-zero): The intervals where $E(x) < 0$ are $(-\infty, -6)$ and $(5, \infty)$. The point where $E(x) = 0$ is $x = -6$. So, the solution set where $E(x) \leq 0$ is $(-\infty, -6] \cup (5, \infty)$. We must exclude the values $x \in \{1, 5, -4, 2\}$.

• $x=-4$ is not in $(-\infty, -6] \cup (5, \infty)$.
• $x=1$ is not in $(-\infty, -6] \cup (5, \infty)$.
• $x=2$ is not in $(-\infty, -6] \cup (5, \infty)$.
• $x=5$ is the boundary of $(5, \infty)$ and must be excluded.

Therefore, the final solution set is $(-\infty, -6] \cup (5, \infty)$.