Question
Question: Solve: $\frac{dy}{dx} = \frac{x+2y-3}{2x+y-3}$...
Solve: dxdy=2x+y−3x+2y−3
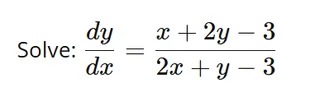
x+y-2 = C(x-y)^3
Solution
The given differential equation is of the form dxdy=a′x+b′y+c′ax+by+c.
-
Check for Intersection of Lines: The lines are x+2y−3=0 and 2x+y−3=0. Their slopes are −1/2 and −2, respectively. Since the slopes are different, the lines intersect.
-
Find the Point of Intersection: Solving the system: h+2k−3=0 2h+k−3=0 From the first equation, h=3−2k. Substituting into the second: 2(3−2k)+k−3=0⟹6−4k+k−3=0⟹3−3k=0⟹k=1. Then h=3−2(1)=1. The point of intersection is (h,k)=(1,1).
-
Substitution: Let x=X+1 and y=Y+1. Then dxdy=dXdY. Substituting into the differential equation: dXdY=2(X+1)+(Y+1)−3(X+1)+2(Y+1)−3=2X+2+Y+1−3X+1+2Y+2−3=2X+YX+2Y
-
Solve the Homogeneous Equation: This is a homogeneous equation. Let Y=vX, so dXdY=v+XdXdv. v+XdXdv=2X+(vX)X+2(vX)=2+v1+2v XdXdv=2+v1+2v−v=2+v1+2v−v(2+v)=2+v1−v2
-
Separate Variables: 1−v22+vdv=XdX
-
Integrate Both Sides: Using partial fractions for the left side: (1−v)(1+v)2+v=1−v3/2+1+v1/2. ∫(1−v3/2+1+v1/2)dv=∫X1dX −23ln∣1−v∣+21ln∣1+v∣=ln∣X∣+C1 Multiplying by 2: −3ln∣1−v∣+ln∣1+v∣=2ln∣X∣+2C1 ln(1−v)31+v=ln(X2)+C2 (1−v)31+v=CX2
-
Substitute Back: Substitute v=Y/X: (1−Y/X)31+Y/X=CX2⟹((X−Y)/X)3(X+Y)/X=CX2 XX+Y⋅(X−Y)3X3=CX2⟹(X−Y)3X2(X+Y)=CX2 Assuming X=0: (X−Y)3X+Y=C⟹X+Y=C(X−Y)3 Substitute back X=x−1 and Y=y−1: (x−1)+(y−1)=C((x−1)−(y−1))3 x+y−2=C(x−y)3
Note on Singular Solutions: The cases 1−v2=0 (i.e., v=1 or v=−1) lead to singular solutions y=x and y=−x+2. The solution y=−x+2 is included in the general solution when C=0. The solution y=x is a singular solution. The question asks for the general solution.
