Question
Question: Solve : $\frac{dy}{dx} = \frac{\sqrt{1-y^2}}{y}$...
Solve : dxdy=y1−y2
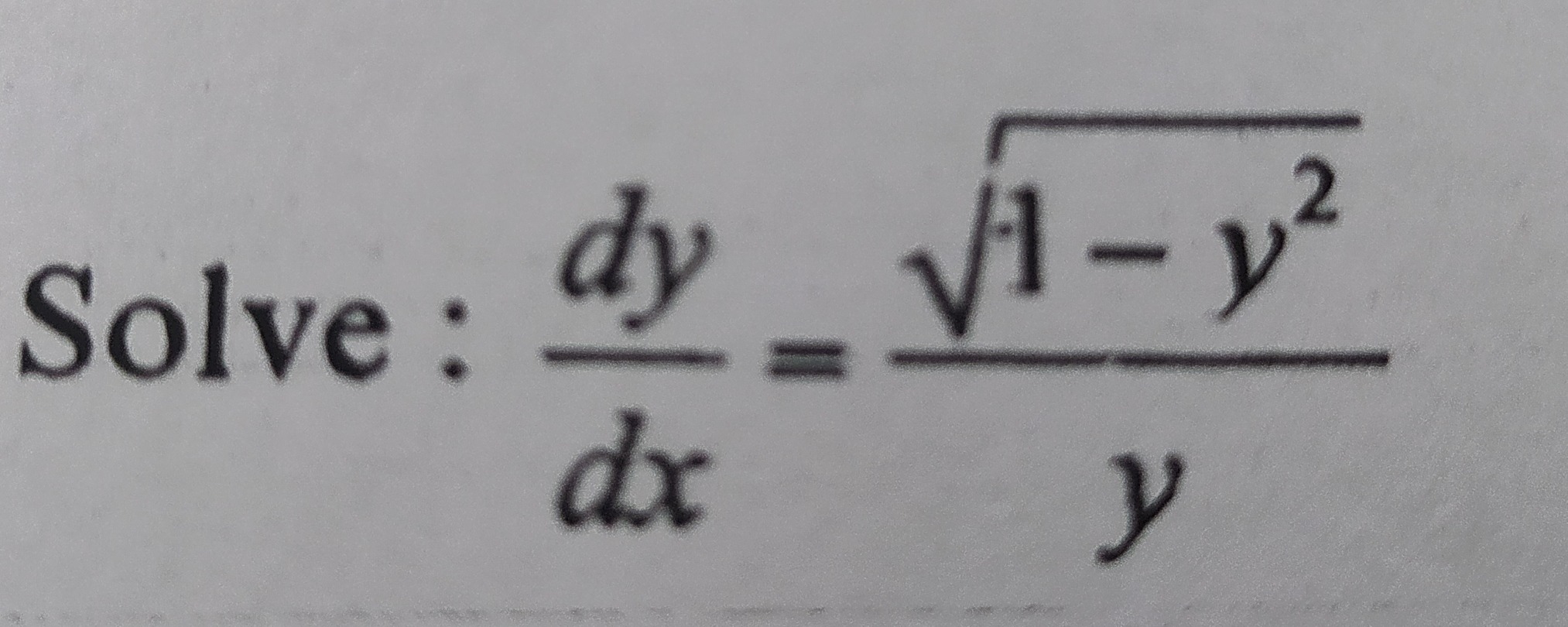
Answer
x+1−y2=C
Explanation
Solution
The given differential equation is separable. Separate variables y and x to opposite sides of the equation. Integrate ∫1−y2ydy using substitution u=1−y2, which yields −1−y2. Integrate ∫dx which yields x. Equate the results and combine constants to get the general solution x+1−y2=C.
