Question

Solve $\frac{dy}{dx} + \frac{2x+1}{x}y = e^{-2x}$.

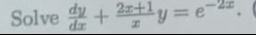
Answer 1

The general solution is $y = e^{-2x} \left(\frac{x}{2} + \frac{C}{x}\right)$.

Answer 2

The differential equation is a first-order linear ODE. The solution is found by calculating the integrating factor $I.F. = e^{\int P(x) dx}$, where $P(x) = \frac{2x+1}{x}$. After finding $I.F. = |x|e^{2x}$, the equation is transformed into $\frac{d}{dx}(y \cdot I.F.) = Q(x) \cdot I.F.$. Integrating both sides yields $y \cdot I.F. = \int Q(x) \cdot I.F. dx + C$. Evaluating $\int |x|dx$ leads to a piecewise integration. The general solution is obtained by combining these cases into $y = e^{-2x} (\frac{x}{2} + \frac{C}{x})$.