Question
Question: Solve for 'x': $-1 \leq \frac{1+x^2}{2x} \leq 1$...
Solve for 'x': −1≤2x1+x2≤1
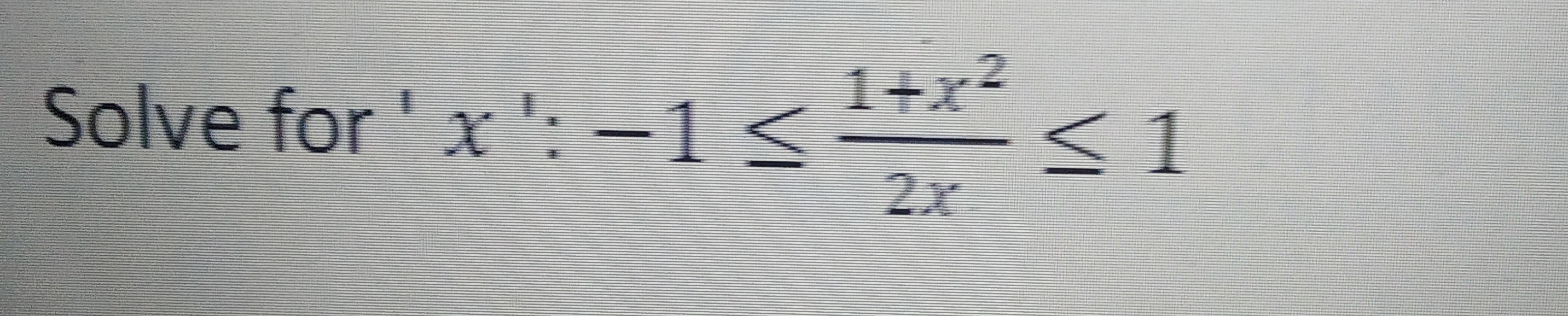
Answer
x ∈ {-1, 1}
Explanation
Solution
The compound inequality −1≤2x1+x2≤1 is equivalent to ∣2x1+x2∣≤1. Since 1+x2≥0, this simplifies to 2∣x∣1+x2≤1. Rearranging gives x2−2∣x∣+1≤0. Let y=∣x∣, so y2−2y+1≤0, which is (y−1)2≤0. Since a square must be non-negative, the only possibility is (y−1)2=0, which means y=1. Substituting back ∣x∣=y, we get ∣x∣=1, which implies x=1 or x=−1. These values satisfy the condition x=0.
