Question
Question: Solve: $e^{x+y}dx + dy = 0$...
Solve: ex+ydx+dy=0
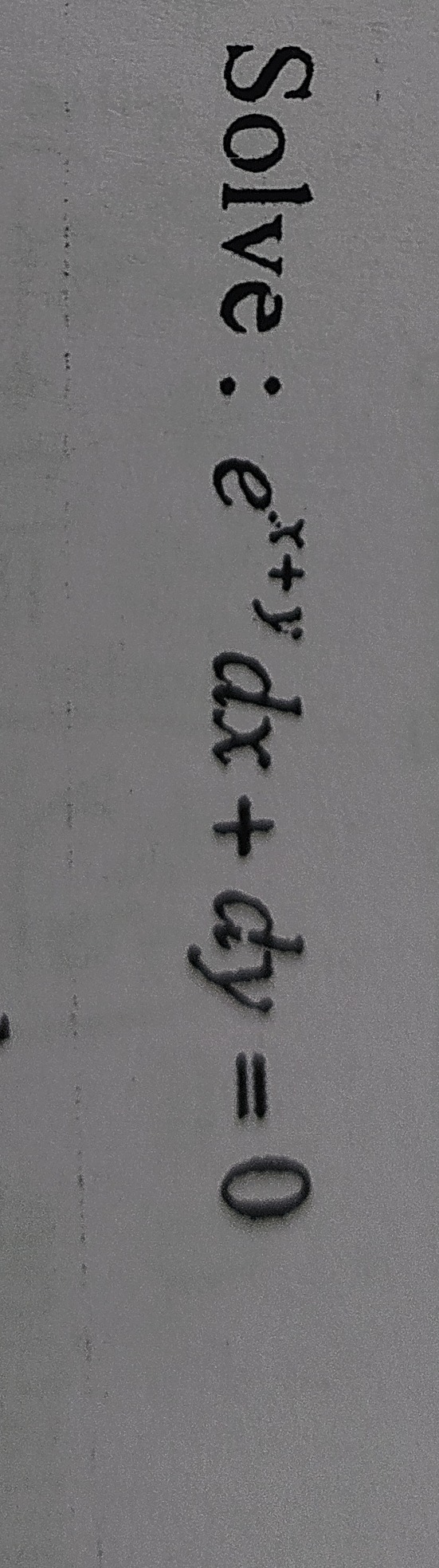
y = -\ln(e^x + K)
Solution
The given differential equation is: ex+ydx+dy=0
Step 1: Separate the variables. First, rewrite the term ex+y as exey. So the equation becomes: exeydx+dy=0
Move the exeydx term to the right side: dy=−exeydx
Now, separate the variables by dividing both sides by ey (note that ey is never zero): eydy=−exdx This can be written as: e−ydy=−exdx
Step 2: Integrate both sides. Integrate both sides of the separated equation: ∫e−ydy=∫−exdx
For the left side integral: ∫e−ydy=−e−y
For the right side integral: ∫−exdx=−ex
Combining the results and adding the constant of integration, C: −e−y=−ex+C
Step 3: Solve for y. Multiply the entire equation by -1 to make the terms positive, or rearrange: e−y=ex−C Since C is an arbitrary constant, −C is also an arbitrary constant. Let's denote it as K for clarity, so K=−C. e−y=ex+K
To solve for y, take the natural logarithm (ln) of both sides: ln(e−y)=ln(ex+K) −y=ln(ex+K)
Finally, multiply by -1 to get y: y=−ln(ex+K)
Here, K is an arbitrary constant of integration. For the logarithm to be defined, ex+K>0.
The final solution is: y=−ln(ex+K)
