Question

Solve: $(cos(x-y))(dx+dy)+(cos(x+y))(dx-dy)=0$

Answer 1

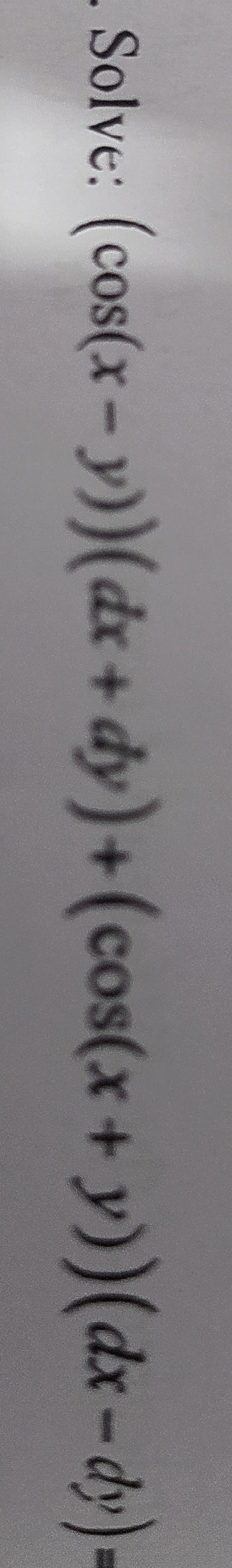
sin(x)=Kcos(y)

Answer 2

The given differential equation is: $(cos(x-y))(dx+dy)+(cos(x+y))(dx-dy)=0$

Step 1: Expand and group terms First, expand the equation: $cos(x-y)dx + cos(x-y)dy + cos(x+y)dx - cos(x+y)dy = 0$

Group the terms containing $dx$ and $dy$: $[cos(x-y) + cos(x+y)]dx + [cos(x-y) - cos(x+y)]dy = 0$

Step 2: Apply trigonometric sum-to-product formulas Use the following trigonometric identities:

1. $cos A + cos B = 2 cos\left(\frac{A+B}{2}\right) cos\left(\frac{A-B}{2}\right)$
2. $cos A - cos B = -2 sin\left(\frac{A+B}{2}\right) sin\left(\frac{A-B}{2}\right)$

For the $dx$ coefficient, let $A = x-y$ and $B = x+y$: $\frac{A+B}{2} = \frac{(x-y)+(x+y)}{2} = \frac{2x}{2} = x$ $\frac{A-B}{2} = \frac{(x-y)-(x+y)}{2} = \frac{-2y}{2} = -y$ So, $cos(x-y) + cos(x+y) = 2 cos(x) cos(-y) = 2 cos(x) cos(y)$

For the $dy$ coefficient, using the same $A$ and $B$: $cos(x-y) - cos(x+y) = -2 sin(x) sin(-y) = -2 sin(x) (-sin(y)) = 2 sin(x) sin(y)$

Substitute these back into the differential equation: $[2 cos(x) cos(y)]dx + [2 sin(x) sin(y)]dy = 0$

Divide the entire equation by 2: $cos(x) cos(y)dx + sin(x) sin(y)dy = 0$

Step 3: Separate the variables This is a separable differential equation. To separate variables, divide the entire equation by $sin(x)cos(y)$: $\frac{cos(x) cos(y)}{sin(x) cos(y)}dx + \frac{sin(x) sin(y)}{sin(x) cos(y)}dy = 0$ $\frac{cos(x)}{sin(x)}dx + \frac{sin(y)}{cos(y)}dy = 0$ $cot(x)dx + tan(y)dy = 0$

Step 4: Integrate both sides Integrate each term with respect to its variable: $\int cot(x)dx + \int tan(y)dy = \int 0$

Recall the standard integrals: $\int cot(x)dx = ln|sin(x)| + C_1$ $\int tan(y)dy = -ln|cos(y)| + C_2$

So, the integral becomes: $ln|sin(x)| - ln|cos(y)| = C$ (where $C = C_3 - C_1 - C_2$ is an arbitrary constant)

Step 5: Simplify the solution Use the logarithm property $ln A - ln B = ln(A/B)$: $ln\left|\frac{sin(x)}{cos(y)}\right| = C$

To remove the logarithm, exponentiate both sides: $\left|\frac{sin(x)}{cos(y)}\right| = e^C$

Let $e^C = K_1$, where $K_1$ is an arbitrary positive constant. $\left|\frac{sin(x)}{cos(y)}\right| = K_1$

This implies $\frac{sin(x)}{cos(y)} = \pm K_1$. Let $K = \pm K_1$ be an arbitrary non-zero constant. $\frac{sin(x)}{cos(y)} = K$

Rearrange to get the final solution: $sin(x) = K cos(y)$

Note: If $K=0$, then $sin(x)=0$, which means $x=n\pi$ for integer $n$. Substituting $x=n\pi$ into the original equation leads to $0=0$, so $x=n\pi$ is also a valid solution, which is covered by $K=0$. Thus, $K$ can be any real constant.

The final solution is $sin(x) = K cos(y)$.