Question

Which of the following curves represents the Henry's law?

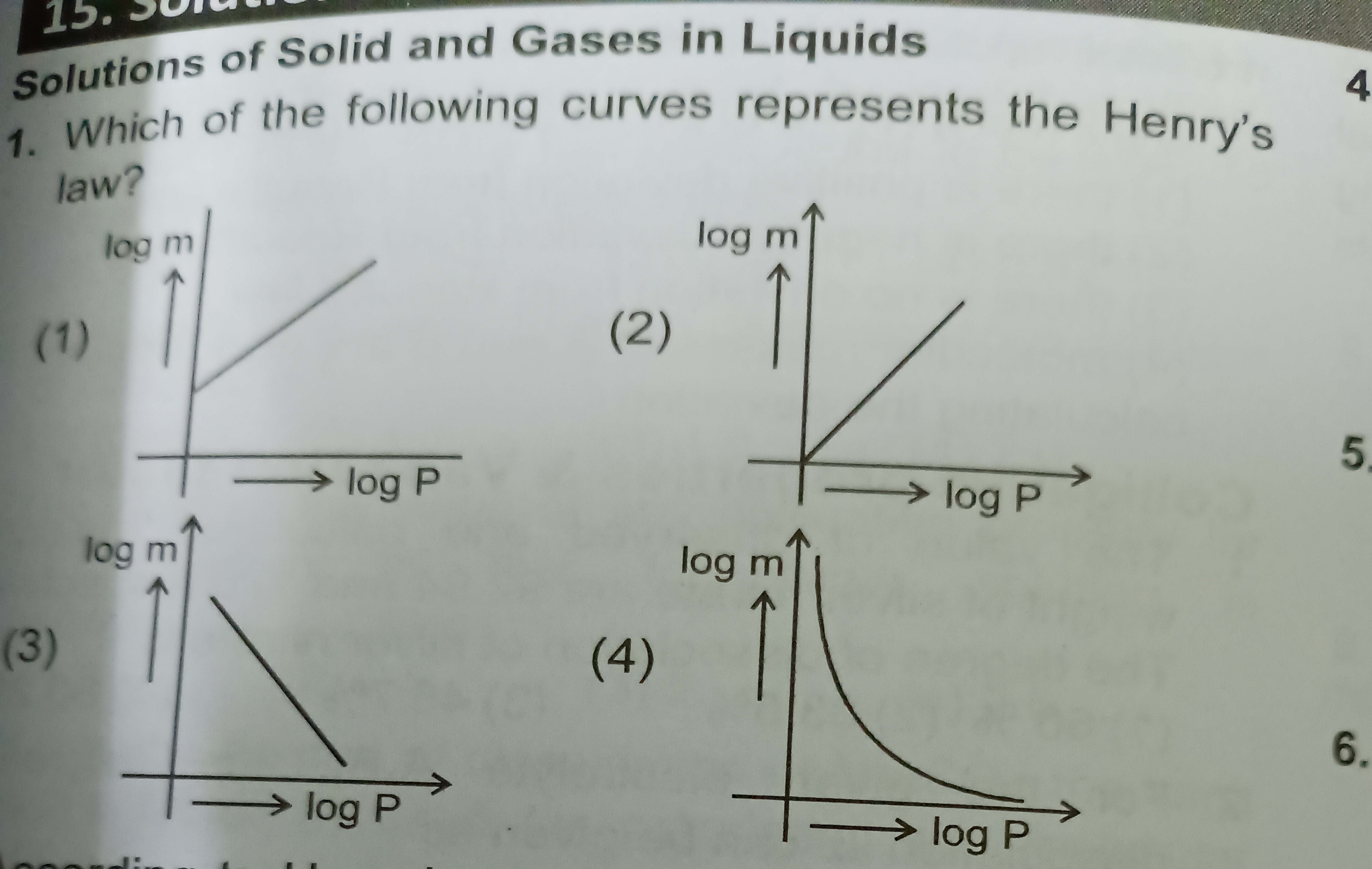
• A. Graph (1): Shows a straight line with a positive slope and a positive y-intercept.
• B. Graph (2): Shows a straight line with a positive slope passing through the origin (zero y-intercept).
• C. Graph (3): Shows a straight line with a negative slope.
• D. Graph (4): Shows a curve, not a straight line.

Answer 1

Answer: (A)

Graph (1): Shows a straight line with a positive slope and a positive y-intercept.

Answer 2

Henry's Law states that the partial pressure of a gas in the vapor phase ($P$) is proportional to the mole fraction of the gas ($x$) in the solution.

$P = K_H x$

where $K_H$ is Henry's Law constant.

Rearranging this equation to express the solubility (or concentration, represented by 'm' in the question) in terms of pressure:

$x = \frac{1}{K_H} P$

Let 'm' represent the solubility or concentration of the gas in the liquid, so $m \propto P$. We can write this as:

$m = k P$

where $k = \frac{1}{K_H}$ is a proportionality constant.

To represent this relationship on a log-log plot (i.e., $\log m$ vs $\log P$), we take the logarithm of both sides of the equation $m = kP$:

$\log m = \log (kP)$

Using the logarithm property $\log(AB) = \log A + \log B$:

$\log m = \log k + \log P$

This equation is in the form of a linear equation $Y = c + X$, where:

$Y = \log m$ (on the y-axis) $X = \log P$ (on the x-axis) $c = \log k$ (the y-intercept)

The slope of this line is 1.

Graph (1) represents the most general case where the constant $k$ can have any positive value, leading to a non-zero intercept ($\log k$).