Question
Question: Solution set of inequality $\sin^3 x \cos x > \cos^3 x \sin x$, where $x \in (0, \pi)$, is...
Solution set of inequality sin3xcosx>cos3xsinx, where x∈(0,π), is
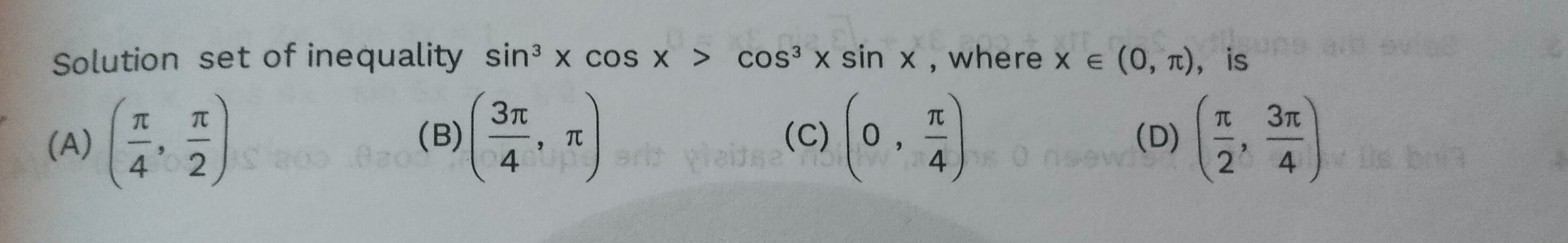
(4π,2π)
(43π,π)
(0,4π)
(2π,43π)
(A) (4π,2π) (B) (43π,π)
Solution
To solve the inequality sin3xcosx>cos3xsinx for x∈(0,π), we proceed as follows:
-
Rearrange the inequality: sin3xcosx−cos3xsinx>0
-
Factor out common terms: sinxcosx(sin2x−cos2x)>0
-
Apply trigonometric identities: We know that sinxcosx=21sin(2x) and sin2x−cos2x=−(cos2x−sin2x)=−cos(2x). Substitute these into the inequality: (21sin(2x))(−cos(2x))>0 −21sin(2x)cos(2x)>0
-
Simplify further using double angle identity: We know that sin(2A)cos(2A)=21sin(4A). Let A=x. So, sin(2x)cos(2x)=21sin(4x). Substitute this back: −21(21sin(4x))>0 −41sin(4x)>0
-
Isolate sin(4x): Multiply by -4 (and reverse the inequality sign): sin(4x)<0
-
Determine the range for 4x: The given domain for x is (0,π). Therefore, the domain for 4x is (4×0,4×π), which is (0,4π).
-
Find intervals where sin(4x)<0 within (0,4π): The sine function is negative in the third and fourth quadrants. For y∈(0,4π), sin(y)<0 when:
- y∈(π,2π)
- y∈(3π,4π)
-
Substitute back y=4x and solve for x: Case 1: π<4x<2π Divide by 4: 4π<x<42π 4π<x<2π
Case 2: 3π<4x<4π Divide by 4: 43π<x<44π 43π<x<π
-
Combine the solutions: The solution set for x∈(0,π) is the union of these two intervals: x∈(4π,2π)∪(43π,π).
Thus, the solution set is (4π,2π)∪(43π,π). Both options (A) and (B) represent parts of this solution.
