Question

Solution of differential equation $2xy \frac{dy}{dx} = x^2 + 3y^2$ is

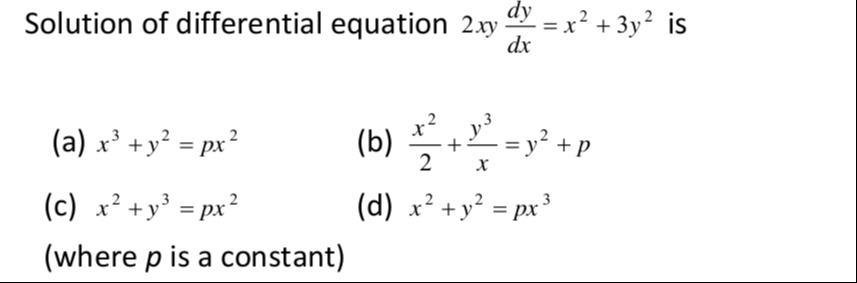
• A. $x^3 + y^2 = px^2$
• B. $\frac{x^2}{2} + \frac{y^3}{x} = y^2 + p$
• C. $x^2 + y^3 = px^2$
• D. $x^2 + y^2 = px^3$

Answer 1

Answer: (D)

$x^2 + y^2 = px^3$

Answer 2

The given differential equation is $2xy \frac{dy}{dx} = x^2 + 3y^2$.

Rearrange it to $\frac{dy}{dx} = \frac{x^2 + 3y^2}{2xy}$.

This is a homogeneous differential equation as the numerator and denominator are homogeneous functions of degree 2.

Substitute $y = vx$, so $\frac{dy}{dx} = v + x \frac{dv}{dx}$.

The equation becomes $v + x \frac{dv}{dx} = \frac{x^2 + 3(vx)^2}{2x(vx)} = \frac{x^2(1+3v^2)}{2vx^2} = \frac{1+3v^2}{2v}$.

$x \frac{dv}{dx} = \frac{1+3v^2}{2v} - v = \frac{1+3v^2-2v^2}{2v} = \frac{1+v^2}{2v}$.

Separate variables: $\frac{2v}{1+v^2} dv = \frac{1}{x} dx$.

Integrate both sides: $\int \frac{2v}{1+v^2} dv = \int \frac{1}{x} dx$.

$\ln|1+v^2| = \ln|x| + \ln|p|$ (where $p$ is the integration constant).

$\ln(1+v^2) = \ln|px|$ (since $1+v^2 > 0$).

$1+v^2 = px$.

Substitute back $v = \frac{y}{x}$:

$1 + \left(\frac{y}{x}\right)^2 = px$

$1 + \frac{y^2}{x^2} = px$

Multiply by $x^2$:

$x^2 + y^2 = px^3$.