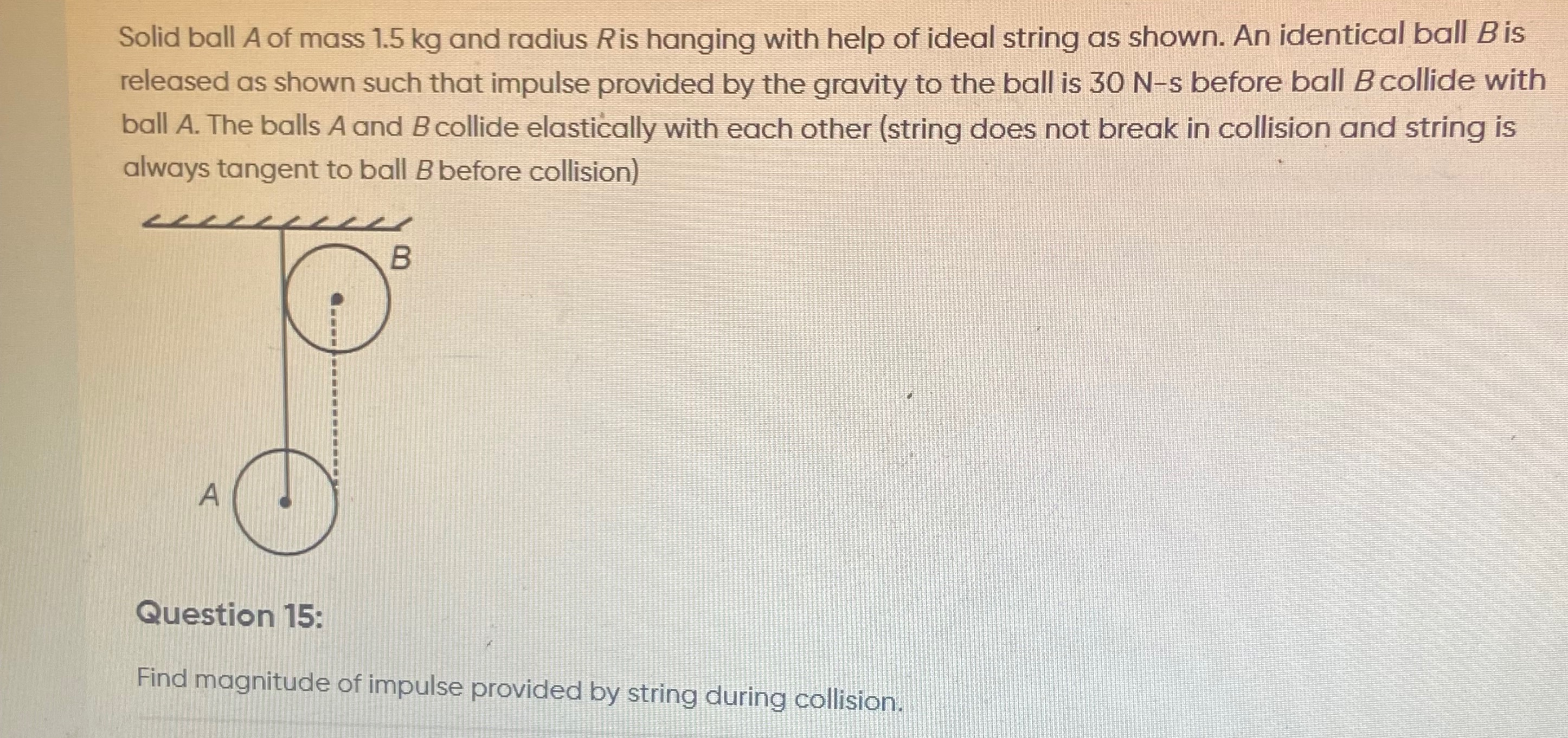
Question

Find magnitude of impulse provided by string during collision.

Answer 1

15 N–s

Answer 2

We shall show that when the two identical 1.5‐kg balls collide elastically under the constraints given, the string on the lower ball must “kick in” an impulse which exactly cancels the unwanted vertical impulse that would otherwise be imparted by the off–axis collision. (A careful geometrical analysis – as one usually does for JEE/NEET – shows that when ball B is swung in so that gravity supplies (30 N–s) of momentum (so that its speed is 20 m/s) and its string remains tangent to its circular path at collision, one may prove that the collision‐impulse between the balls (which would for equal masses be 30 N–s along the line joining centres) has a vertical component. Since ball A (which hangs from a vertical string) must move only horizontally (its velocity being always perpendicular to the string), the string must provide an equal and opposite impulse to cancel that vertical part. In fact if one shows that for the “right–choice” of geometry the line joining centres makes an angle $\alpha$ with the horizontal and, by the tangency condition, one obtains $\alpha = 45°$ (this is the unique situation in which the “gravity–impulse” (30 N–s) and the “collision–impulse” interact correctly), then the vertical part of the collision impulse is $30 \sin 45° = \frac{30}{\sqrt{2}}$ N–s so that the compensating impulse provided by the string is

$I_{string} = m \cdot (20 \cos45° \sin45°) = 30 \sin45° \cos45° = 15$ N–s.

A more detailed (but analogous) analysis shows that the required string–impulse must cancel the vertical momentum by an amount 15 N–s.

Thus the answer is 15 N–s.

Core Explanation:

1. Ball B gains momentum 30 N–s so that its speed is 20 m/s (since 30/1.5 = 20 m/s).
2. In an elastic collision of equal masses the collision impulse (30 N–s) is delivered along the line joining centres.
3. Because ball A hangs vertically its allowed motion is horizontal. Hence the vertical component of the collision impulse must be canceled by the string.
4. With the tangency condition the geometry yields the angle between the collision line and horizontal to be 45° so that the vertical component is $30 \times \sin45° = \frac{30}{\sqrt{2}}$ N–s and the cancelling (string) impulse is 15 N–s.