Question
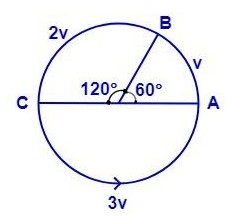
Question: Sohail cycles on a circular track in anticlockwise direction as shown in the figure. He travels with...
Sohail cycles on a circular track in anticlockwise direction as shown in the figure. He travels with a speed ‘v’ to cover the path AB, next with speed ‘2v’ from B to C and with a speed of ‘3v’ from C to A. What is the average speed for the total journey?
Solution
Use the distance formula of circle i.e.
d=2πr360∘θ
Where d is the distance travelled in θ angle and r is the radius of the circle.
When the distance travelled in each segment of the circle is found use the given velocities to calculate the time taken to travel each segment.
After that use the average speed formula:
Average speed=Total timeTotal distance
Or
vavg=TD
Where D is the total distance travelled and T is the total time taken to travel the same distance.
Complete step by step solution

Distance travelled from A to B
d1=2πr360∘60∘d1=62πr
Time taken from A to B
t1=v1d1t1=6v2πrt1=3vπr
Distance travelled from B to C
d2=2πr360∘120∘d2=32πr
Time taken from B to C
t2=v2d2t2=3(2v)2πrt2=3vπr
Distance travelled from C to A
d3=2πr360∘180∘d3=22πrd3=πr
Time taken from C to A
t3=v3d3t3=3vπr
Average speed of the total journey:
Average speed=Total timeTotal distance
vavg=t1+t2+t3d1+d2+d3=3vπr+3vπr+3vπr2πr=3v3πr2πrvavg=2v
Therefore, the average speed of the total journey is 2v.
Note
Always remember to calculate the time of each segment separately to avoid the confusion during the calculation of average speed collectively at last. Distance travelled during motion and displacement can be different. So while calculating distance we have to consider the full path of journey.
