Question

Sketch the region common to the circle ${x^2} + {y^2} = 16$ and the parabola ${x^2} = 6y$. Also, find the area of the region, using integration.

Answer 1

Here we will first find the points of the intersection of the two curves by putting the parabola equation in the equation of the circle. Then we will draw the required figure and show the bounded region. We will use the basics of the integration to find the area of the bounded region and simplify the equation to get the area of the bounded region in the simplified form.

Complete Step by Step Solution:
Given equation of circle is ${x^2} + {y^2} = 16$………………………..$\left( 1 \right)$
Equation of the given parabola is ${x^2} = 6y$………………………..$\left( 2 \right)$
Now we will use the equation $\left( 2 \right)$ in equation $\left( 1 \right)$ to get the points of the intersection of the curve. Therefore, we get
$6y + {y^2} = 16$
$\Rightarrow {y^2} + 6y - 16 = 0$
The above equation is a quadratic equation, we will solve this equation to get the value of $y$.
Factoring the above equation, we get
$\Rightarrow {y^2} + 8y - 2y - 16 = 0$
$\Rightarrow \left( {y + 8} \right)\left( {y - 2} \right) = 0$
Applying zero product property, we get
$\begin{array}{l} \Rightarrow \left( {y + 8} \right) = 0\\\ \Rightarrow y = - 8\end{array}$
Or
$\begin{array}{l} \Rightarrow \left( {y - 2} \right) = 0\\\ \Rightarrow y = 2\end{array}$
Hence the value of $y$ is $y = - 8,y = 2$. Now we will find the value of $x$ using the value of $y$, we get
If $y = 2$ then the value of $x$ is
${x^2} = 6 \times 2 = 12$
$\Rightarrow x = \pm \sqrt {12} = \pm 2\sqrt 3$
If the value of $y = - 8$, then the value of $x$ is
${x^2} = 6 \times \left( { - 8} \right) = - 48$
So the value in case of $y = - 8$ is imaginary. Therefore, the points of intersection of the circle and the parabola is $\left( {2\sqrt 3 ,2} \right),\left( { - 2\sqrt 3 ,2} \right)$.
Now we will draw the figure of the given condition and shade the common region, we get

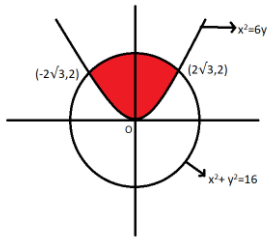
Now we will find the area bounded by using the integration. Therefore, we get
Area of the bounded region$= \int\limits_{ - 2\sqrt 3 }^{2\sqrt 3 } {\left[ {\left( {\sqrt {16 - {x^2}} } \right) - \dfrac{{{x^2}}}{6}} \right]} dx$
Now we will solve this equation using the integration to get the value of the area of the bounded region. We can write the above equation in other form by using the property of the integration, we get
$\Rightarrow$ Area of the bounded region $= 2\int\limits_0^{2\sqrt 3 } {\left[ {\left( {\sqrt {16 - {x^2}} } \right) - \dfrac{{{x^2}}}{6}} \right]} dx$
$\Rightarrow$ Area of the bounded region $= 2\left[ {\int\limits_0^{2\sqrt 3 } {\left( {\sqrt {16 - {x^2}} } \right)} dx - \int\limits_0^{2\sqrt 3 } {\dfrac{{{x^2}}}{6}} } \right]$
Now we will simply integrate the equation, we get
$\Rightarrow$ Area of the bounded region $= 2\left[ {\dfrac{{x\sqrt {{4^2} - {x^2}} }}{2} + \dfrac{{{4^2}}}{2}{{\sin }^{ - 1}}\left( {\dfrac{x}{4}} \right) - \left( {\dfrac{1}{6} \times \dfrac{{{x^3}}}{3}} \right)} \right]_0^{2\sqrt 3 }$
Now we will put the limit in the variable to get the final equation. So, we get
$\Rightarrow$ Area of the bounded region $= 2\left[ {\dfrac{{\left( {2\sqrt 3 } \right)\sqrt {{4^2} - {{\left( {2\sqrt 3 } \right)}^2}} }}{2} + \dfrac{{{4^2}}}{2}{{\sin }^{ - 1}}\left( {\dfrac{{2\sqrt 3 }}{4}} \right) - \left( {\dfrac{1}{6} \times \dfrac{{{{\left( {2\sqrt 3 } \right)}^3}}}{3}} \right)} \right]$
$\Rightarrow$ Area of the bounded region $= 2\left[ {\dfrac{{\left( {2\sqrt 3 } \right)\sqrt {16 - 12} }}{2} + \dfrac{{{4^2}}}{2}{{\sin }^{ - 1}}\left( {\dfrac{{\sqrt 3 }}{2}} \right) - \left( {\dfrac{1}{6} \times \dfrac{{8 \times 3 \times \sqrt 3 }}{3}} \right)} \right]$
Dividing the terms, we get
$\Rightarrow$ Area of the bounded region $= 2\left[ {\sqrt 3 \times \sqrt 4 + \dfrac{{{4^2}}}{2}{{\sin }^{ - 1}}\left( {\sin \dfrac{\pi }{3}} \right) - \left( {\dfrac{{4 \times \sqrt 3 }}{3}} \right)} \right]$
Applying the exponent on the terms, we get
$\Rightarrow$ Area of the bounded region $= 2\left[ {2\sqrt 3 + \dfrac{{16}}{2} \times \dfrac{\pi }{3} - \left( {\dfrac{{4\sqrt 3 }}{3}} \right)} \right]$
$\Rightarrow$Area of the bounded region $= 2\left[ {2\sqrt 3 + \dfrac{{8\pi }}{3} - \left( {\dfrac{{4\sqrt 3 }}{3}} \right)} \right]$
Now we will take the LCM inside the brackets, we get
$\Rightarrow$ Area of the bounded region $= 2\left[ {\dfrac{{6\sqrt 3 + 8\pi - 4\sqrt 3 }}{3}} \right]$
Subtracting the like terms, we get
$\Rightarrow$ Area of the bounded region $= 2\left[ {\dfrac{{2\sqrt 3 + 8\pi }}{3}} \right]$
Multiplying the terms, we get
$\Rightarrow$ Area of the bounded region $= \dfrac{{4\sqrt 3 + 16\pi }}{3}$
$\Rightarrow$ Area of the bounded region $= \dfrac{4}{3}\left( {\sqrt 3 + 4\pi } \right)$

Hence, the value of the area of the bounded region, using integration is $\dfrac{4}{3}\left( {\sqrt 3 + 4\pi } \right)$ sq. units.

Note:
While calculating the area of the bounded region we should subtract the area of the parabola as the region is bounded in between the curves only. We should write the proper coordinates of the intersection of the curves on the Cartesian plane as it is used to get the limits of the integration part of the equation to find out the area of the bounded region. While writing the coordinates of a point always the X-axis intercept of the point is written first and then the Y-axis intercept is written. Also in the representation of this axis in the Cartesian plane are perpendicular to each other and intersecting at a point which is named as the origin.