Question

Sketch the graph $y = \left| {x - 1} \right|$ . Evaluate $\int\limits_{ - 2}^4 {\left| {x - 1} \right|} dx$ . What does this value of the integral represent on the graph?

Answer 1

Hint : Integration is the process of finding the antiderivative. Finding the integral of a function with respect to x means finding the area to the x axis from the curve. The integral is usually called the antiderivative, because integrating is the reverse process of differentiating. To evaluate $\int\limits_{ - 2}^4 {\left| {x - 1} \right|} dx$ we need to find the integration of the given function such that the range is from -2 to 4, hence evaluate based on the given interval.

Complete step-by-step answer :
Let us write the given data,
We need to sketch the graph for: $y = \left| {x - 1} \right|$ and Evaluate $\int\limits_{ - 2}^4 {\left| {x - 1} \right|} dx$ .
As the range of the integral given is from -2 to 4, hence we get:
$\int\limits_{ - 2}^4 {\left| {x - 1} \right|} dx$ = $\int\limits_{ - 2}^1 {\left| {x - 1} \right|} + \int\limits_1^4 {\left| {x - 1} \right|}$
$\left| {x - 1} \right|$ for $x < 1$ , $1 - x$
$\left| {x - 1} \right|$ for $x > 1$ , $x - 1$
Hence, we get the equation as:
$\Rightarrow$ $\int\limits_{ - 2}^1 {\left( {1 - x} \right)dx} + \int\limits_1^4 {\left( {x - 1} \right)dx}$
Apply the integrals, we get
$\Rightarrow$ $\left[ {x - \dfrac{x{^2}}{2}} \right] _{ - 2}^1 + \left[ {\dfrac{{{x^2}}}{2} - x} \right] _1^4$
Now, find the integration of the terms as:
$\Rightarrow$ $\left[ {\left( {1 - \dfrac{1}{2}} \right) - \left( { - 2 - \dfrac{4}{2}} \right)} \right] + \left[ {\left( {\dfrac{{{4^2}}}{2}} \right) - \left( {\dfrac{1}{2}} \right) - 1} \right]$
$\Rightarrow$ $\left[ {\dfrac{1}{2} + 4} \right] + \left[ {4 + \dfrac{1}{2}} \right]$
$\Rightarrow$ $8 + 1 = 9$ sq. units.
Hence, the graph of $y = \left| {x - 1} \right|$ is represented as:

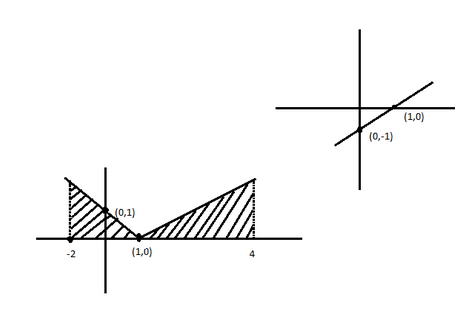
So, the correct answer is “Option B”.

Note : The different methods of integration include:
Integration by Substitution: To find the integration of a function, thus we can find the integration by introducing a new independent variable. This method is called Integration by Substitution.
A.Integration by Parts: Integration by parts requires a special technique for integration of a function, where the integrand function is the multiple of two or more functions.
B.Integration Using Trigonometric Identities: In the integration of a function, if the integrand involves any kind of trigonometric function, then we use trigonometric identities to simplify the function that can be easily integrated.
C.Integration by Partial Fraction: a rational function is defined as the ratio of two polynomials which can be expressed in the form of partial fractions.
D.Integration of Some particular function: Integration of some particular function involves some important formulae of integration that can be applied to make other integration into the standard form of the integrand.