Question

Sketch the graph of $y={{x}^{2}}+8$ and describe the transformation?

Answer 1

Here, the question is about the vertical shift of quadratic function.
As we have to solve this given quadratic equation and have to draw the graph.
But for drawing the graph, we need its $x$ and $y$ coefficient and for that we have to solve the given quadratic equation.
For that we can use the standard equation of quadratic equation that is,
$y=a{{x}^{2}}+bx+c$
Also we can use, the $x$ vertex function as,
${{x}_{vertex}}=\left( -1 \right)\times \dfrac{b}{2a}$
By using this two formulae we can find the $x$ and $y$ intercept of the given equation.

Complete step by step solution:
Given that, the equation is
$y={{x}^{2}}+8...(i)$
The transformation is of ${{x}^{2}}$ but it is raised by $8$ on the $y-$axis.
As we know that the graph is consist of vertex as $x$ and $y$and from equation $\left( i \right)$ it is given as, $(x,y)=(0,8)$
$\therefore$ $x-$intercept $=$ none or zero
$y-$ intercept $=$ 8
Thus the graph will be drawn on $y-$ axis only as the $x-$intercept is zero.

General shape:
Determine the general shape of the graph.
As the given equation is a quadratic equation, it must has a horse shoe type shape.
Also, the ${{x}^{2}}$ term in the given equation is positive that’s why it has the general form of $\cup .$

Axis of symmetry:-
As we know the standard equation of a quadratic equation and it is given as.
$y=a{{x}^{2}}+bx+c....(ii)$
We can also write it as,
$y=a\left( {{x}^{2}}+\dfrac{b}{a}x \right)+c....(iii)$
From above equation, we can use a vertex function that is,
$x$ vertex $=\,\left( -1 \right)\times \dfrac{b}{2a}$
$x$ vertex $=\,\left( \dfrac{-1}{2} \right)\,\times \,\dfrac{b}{a}\,\,\,\,\,\,.....(iv)$
But in equation $\left( ii \right)$ the value of $a$ is,
$a=2$ and $\therefore \,\,\,a{{x}^{2}}=1\times {{x}^{2}}={{x}^{2}}$
Therefore, $\dfrac{b}{a}=\dfrac{b}{1}=1$
Now, compare equation $(i)$ with equation $(ii)$
$\Rightarrow y={{x}^{2}}+8$
\Rightarrow $$$$y=a{{x}^{2}}+bx+c
So, in equation $(i)$ there is no $bx$ term present in the equation, so we can write it as $b=0$.
Now, the equation $(iv)$ becomes.
${{x}_{vetrex}}=\left( -\dfrac{1}{2} \right)\times \dfrac{b}{a}=\left( -\dfrac{1}{2} \right)\times \dfrac{0}{1}=0$
${{x}_{vertex}}=0$
Hence, the ${{x}_{vertex}}=0$, the graph is plotted only on $y$-axis and $y$-axis is the axis symmetry. Determination of $y$-intercept and $x-$intercept. As we already found that the $y$-axis is the axis symmetry$\therefore x=0$.
$\therefore$ According to equation $(i)$
i.e. $y={{x}^{2}}+8$
$\Rightarrow y=0+8$
$\Rightarrow y=0$
$\therefore y$-intercept$=\left( x,y \right)=\left( 0,8 \right)$
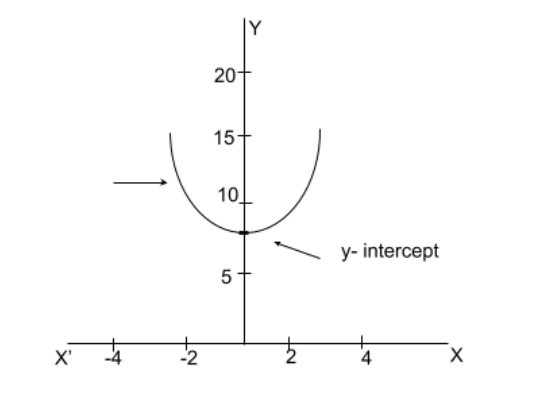
The vertex of graph is $\left( 0,8 \right)$ and as we already found that the graph is in the form of $U$ and it doesn’t have $x-$intercept.

The given graph is represented as:
We already know that the general shape of graph is $U$. And it has points $\left( x,y \right)=\left( 0,8 \right)$ so the representation on graph will be as follows:

Note: In this question, a quadratic equation is given and from that we have to draw the graph.
But actually it is a vertical shift of quadratic graph.
As the given equation is in the form of $y=a{{x}^{2}}+c$
Which is a parabola along with a y-intercept that is $\left( 0,c \right)$.
The vertical shift is nothing but the vertical movement along with the parabola’s line of symmetry. The vertical shift could be determined on the basis of value $c$.
If the value of $c$ is positive then the graph will be shifted upward and if the value of $c$ is negative then the graph will be shifted downward. Always remember to label the graph after drawing. Label the points and also write the title of the graph.