Question

Sketch the graph of $y = {\log _{\dfrac{1}{2}}}x$ and $y = {\left( {\dfrac{1}{2}} \right)^x}$?

Answer 1

We have given two equations. The first equation is a logarithmic function and the second equation is an exponential function. To draw the graph of the logarithmic function, we substitute the positive values of $x$ as the domain of the logarithmic function is as the domain of the logarithmic function is ${R^ + }$ .
To draw the exponential function, we substitute all the real numbers as the domain of the exponential function is $R$ .

Complete step by step solution:
Step 1: We have given two functions: $y = {\log _{\dfrac{1}{2}}}x$ and $y = {\left( {\dfrac{1}{2}} \right)^x}$ . First, we draw the graph of $y = {\log _{\dfrac{1}{2}}}x$. For that, we substitute the different values of $x$ . The following table shows the values of $y$ for different values of $x$.

$x$	$1$	$\dfrac{1}{2}$	$\dfrac{1}{4}$	$\dfrac{1}{8}$	$2$	$4$
$y = {\log _{\dfrac{1}{2}}}x$	${\log _{\dfrac{1}{2}}}1$ $\Rightarrow 0$	${\log _{\dfrac{1}{2}}}\dfrac{1}{2}$ $\Rightarrow 1$	${\log _{\dfrac{1}{2}}}\dfrac{1}{4}$ $\Rightarrow 2$	${\log _{\dfrac{1}{2}}}\dfrac{1}{8}$ $\Rightarrow 3$	${\log _{\dfrac{1}{2}}}2$ $\Rightarrow - 1$	${\log _{\dfrac{1}{2}}}4$ $\Rightarrow - 2$

Step 2: Now we draw the graph of the logarithmic function $y = {\log _{\dfrac{1}{2}}}x$. Following is the graph of $y = {\log _{\dfrac{1}{2}}}x$

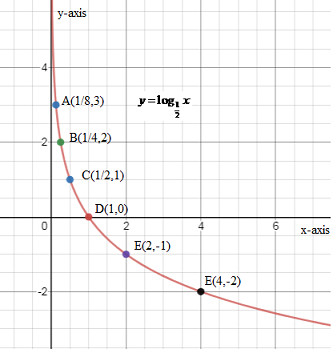
Step 3: Now, we draw the graph of $y = {\left( {\dfrac{1}{2}} \right)^x}$. For that, we substitute the different values of $x$ . The following table shows the values of $y$ for different values of $x$.

$x$	$0$	$1$	$- 1$	$2$	$- 2$	$3$
$y = {\left( {\dfrac{1}{2}} \right)^x}$	${\left( {\dfrac{1}{2}} \right)^0}$ $\Rightarrow 1$	${\left( {\dfrac{1}{2}} \right)^1}$ $\Rightarrow \dfrac{1}{2}$	${\left( {\dfrac{1}{2}} \right)^{ - 1}}$ $\Rightarrow 2$	${\left( {\dfrac{1}{2}} \right)^2}$ $\Rightarrow \dfrac{1}{4}$	${\left( {\dfrac{1}{2}} \right)^{ - 2}}$ $\Rightarrow 4$	${\left( {\dfrac{1}{2}} \right)^3}$ $\Rightarrow \dfrac{1}{8}$

Step 4: Now we draw the graph of the logarithmic function $y = {\left( {\dfrac{1}{2}} \right)^x}$. Following is the graph of $y = {\left( {\dfrac{1}{2}} \right)^x}$.

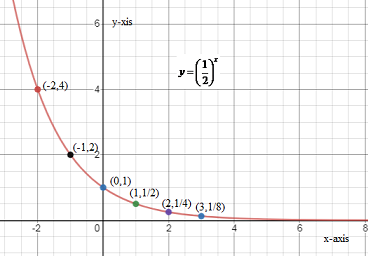
Step 5: The plot of both the function on the same graph is as follows:

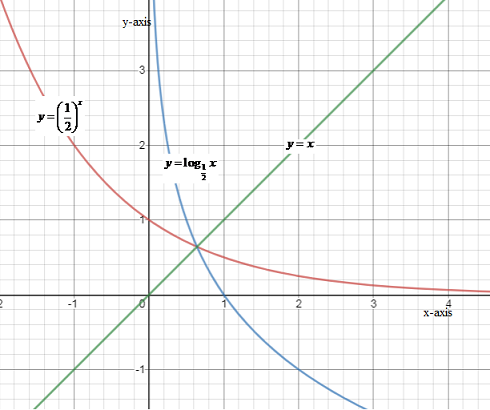
From the above curve, it is clear that both the curves are symmetric about the line $y = x$ .

Note: The logarithmic function is undefined for negative values of $x$ .
The value of the exponential function is always positive.
Graph of the logarithmic function and exponential function is symmetric about the line $y = x$. Choose the values of $x$ such that it is an integer power of the base, so we can determine the value of the logarithmic function.