Question

Sketch the graph for $y = {\tan ^{ - 1}}(\tan x)$

Answer 1

To sketch the graph of $y = {\tan ^{ - 1}}(\tan x)$ . First, we have to calculate the domain and range of tanx and ${\tan ^{ - 1}}$ . From this, we can sketch the graph of $\tan x$ and ${\tan ^{ - 1}}$ . With the help of these, we can draw a graph of $y = {\tan ^{ - 1}}(\tan x)$
In a relation R from set A to set B, the set of all first components of order pair belongings to R is called the domain and all the second element of pair is called range.

Complete step by step solution:
We know that the domain of tan. function(tangent function) is the set \left\\{ {x:x \in R,and.x \ne (2n + 1)\dfrac{\pi }{2},n \in Z} \right\\}
here R represents the real number and $x \ne (2n + 1)\dfrac{\pi }{2}$ means the domain of tan function does not contain an odd multiple of $\dfrac{\pi }{2}$ . $n \in Z$ Represents that n is an integer. Z is the symbol of an integer.
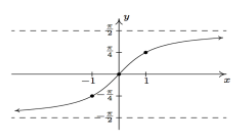
The range of the tan function in R. Here R represents the real number. If we restrict the domain of a tangent function to $\left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right)$ then it is one-one and onto with the range R. So, the tangent function is restricted to any of interval etc, is bijective and range is R. SO, ${\tan ^{ - 1}}$ can be defined as the function whose domain is R and range could be any of interval $\left( {\dfrac{{ - 3\pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right)$ and so on. This interval gives different branches of the function ${\tan ^{ - 1}}$ . The branch $\left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right)$ is called the principal value branch of the function ${\tan ^{ - 1}}$ therefor ${\tan ^{ - 1}}:R \to \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right)$

The graph of a tan function $y = \tan x$ is given as:

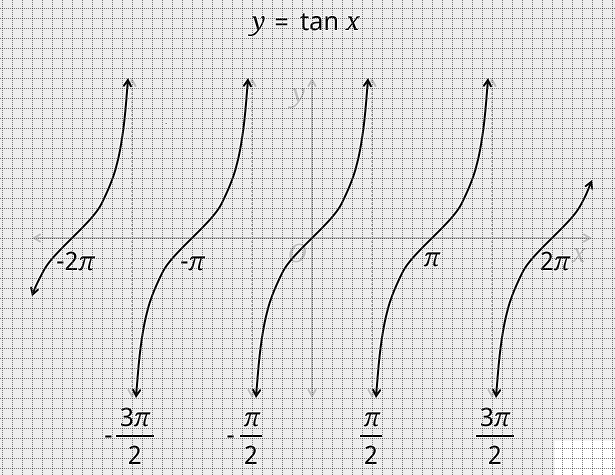
The graph of $y = {\tan ^{ - 1}}x$ is given as

As $y = {\tan ^{ - 1}}(\tan x)$ is periodic with period π. therefore to draw this graph we should draw the graph for one interval $\pi$ and repeat for the entire value.
As we know that $y = {\tan ^{ - 1}}(\tan x)$ = \left\\{ {x:\dfrac{\pi }{2} < x < \dfrac{\pi }{2}} \right\\}
This has been defined for $\dfrac{\pi }{2} < x < \dfrac{\pi }{2}$ that has a length $\pi$ so its graph could be plotted as

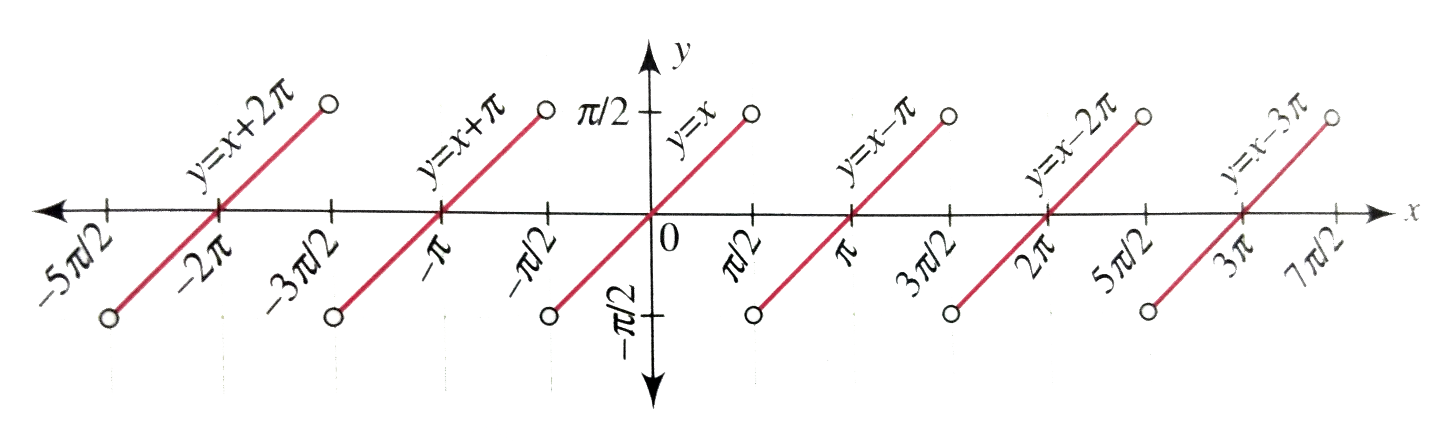
Thus this graph of y where y is not defined for $x \in (2n + 1)\dfrac{\pi }{2}$ .

Note:
One-one function: A function $f:x \to y$ is defined as a one-one function of the image of distinct elements of X under $f$ are distinct.
Onto function: A function is $f:x \to y$ said to be onto the function of every element of Y is an image of some element of X under f.
Bijective Function: The function which is both one-one and onto is called the bijective function.