Question
Question: Sixteen resistors each of resistance 16\(\Omega \) are connected in circuit as shown. Calculate the ...
Sixteen resistors each of resistance 16Ω are connected in circuit as shown. Calculate the net resistance between A and B.
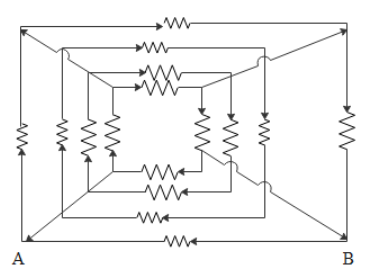
Solution
Here the four resistors R on each side are in parallel. Thus first calculate the equivalent resistance for each side. Then re arrange the diagram using the calculated value. Then we will get a series connection across the resistor AB. Then the series resistor will be parallel to the resistor across AB. Hence, the resultant value of those two parallel resistors will be the net resistance across AB. Hence while calculating the equivalent resistance, first note whether it is connected in series or parallel. Then use the suitable equation of the given circuit.
Complete answer:
Here all resistance is R=16Ω on each parallel side.
Thus equivalent resistance of each side is,
Four resistors are connected parallel on each side.
Hence,
Req1=R1+R1+R1+R1
⇒Req1=R4⇒Req=4R
This is the equivalent resistance for one side. Since the equivalent resistance on four sides are equal, the equivalent resistance on four sides are equal to 4R.
Thus the resultant circuit becomes,
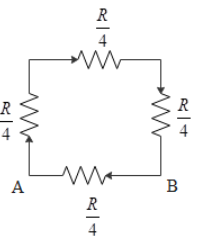
Here the three resistors are connected in series to the resistor connected between AB.
Hence the resistance for the series connection is,
R′=4R+4R+4R⇒R′=43R
Then the resistors R′ and Req becomes parallel.
Thus the resultant circuit becomes,
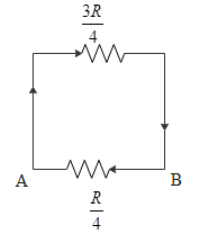
Therefore the net resistance between A and B is,
RAB1=(43R)1+(4R)1
⇒RAB1=3R4+R4⇒RAB1=3R4+3R4×3⇒RAB1=3R16⇒RAB=163R
Given that R=16Ω
Hence,
RAB=163×16⇒RAB=3Ω
Note:
The net resistance in a series connection is the sum of resistances connected in the given circuit. Whereas, the net resistance in a parallel connection, that is the reciprocal of equivalent resistance is the sum of reciprocals of the individual resistances. Hence while calculating the equivalent resistance, first note whether it is connected in series or parallel. Then use the suitable equation of the given circuit.
