Question

Six vectors, $a$ through $f$ have the same magnitudes and directions indicated in the figure, Which of the following statements is true,

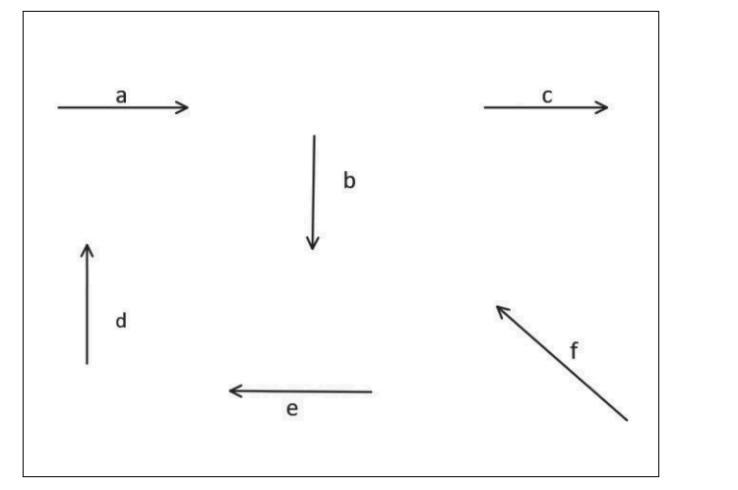
A. $b + e = f$
B. $b + c = f$
C. $d + c = f$
D. $d + e = f$

Answer 1

Hint : The given question actually asks us to find the correct option which will result in the vector $f$ on addition. The vector in question here is $f$ which is pointing towards the north west direction. Since all the given vectors in the question have the same magnitude the only deciding factor between the given vectors will be the direction. For the addition of vectors we use what is called the triangle law of vector addition. In this the starting point of the first vector to the ending point of the second vector are joined to find the direction of the vector after addition.

Complete step-by-step answer :
We will check all the options one by one and check if they are correct or not.
The option A here says
$b + e = f$
But since $b$ points south and $e$ points west the resultant vector would be in the south west direction but our vector $f$ is in the North West direction hence this option is incorrect.
The option B here says,
$b + c = f$
But since $b$ points south and $c$ points east the resultant vector would be in the south east direction but our vector $f$ is in the North West direction hence this option is incorrect.
The option C here says
$d + c = f$
But since $d$ points north and $c$ points east the resultant vector would be in the north east direction but our vector $f$ is in the North West direction hence this option is incorrect.
Thus the only option left which is correct is the D
$d + e = f$
As $d$ points north and $e$ points west the resultant vector would be in the north west direction as our vector $f$ is in the North West direction hence this option is correct.
So, the correct answer is “Option D”.

Note : The vector addition of two vectors can be explained by both the laws,
I.The law of triangle addition.
II.The law of parallelogram addition.